2015-05-05
259
Пусть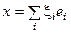 
(разложение в базисе { ei }) и 
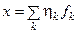(разложение в базисе { fi }), тогда 
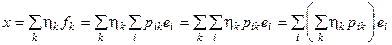. Получены два разложения вектора х в базисе { ei }отсюда 
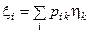, т.е. х (е) = Рх (f) или х (f) = Р –1 х (e).
Преобразование матрицы линейного оператора
Пусть А линейный оператор и А (е) и А (f) – его матрицы в соответствующих базисах.
у (е) = А (е) х (е) Þ Ру (f) = А (e) Рх (f) Þ у (f) = Р –1 А (e) Рх (f)Þ А (f) = Р –1 А (e) Р.
Преобразование коэффициентов линейных форм
Пусть L (x) линейная форма на V. Тогда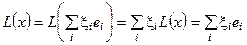 
,
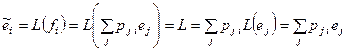т.е.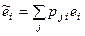 
или e (f) = Pe (e).
Коэффициенты линейной формы при изменении базиса изменяются как базисные векторы.
Преобразование матрицы билинейной формы
Пусть j(х, у) – билинейная форма на V. Т.е.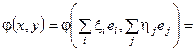 
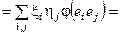
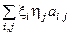где аi j – матрица билинейной формы в базисе { еi }.
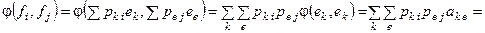
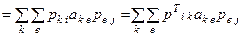, а это значит, что А (f) = PТА (e) Р.
