Пусть А – эрмитов оператор; l1 ³ l2 ³ … ³ l n собственные значения этого оператора и { е 1, е 2, …, еm } – соответствующий им ортонормированный собственный базис. Тогда " x Î V 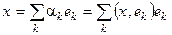 ; Ax =
; Ax = 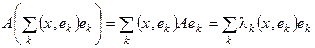 .
.
Def: Оператор Рk: Pkx = (x,ek) ek, называется оператором-проектором или просто проектором на одномерное пространство, порожденное вектором { ek }.
Свойства проекторов:
1°. Pk – самосопряженный (эрмитов).
◀ (Pkx, y) = ((x,ek) ek, y) = (x,ek)(ek,y) = 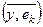 (x, ek) = (x, (y,ek) ek) = (x, Pky) ▶
(x, ek) = (x, (y,ek) ek) = (x, Pky) ▶
2°. 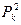 = Pk. ◀
= Pk. ◀ 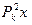 = Pk (Pkx) = Pk (x,ek) ek = (x,ek) Pek = (x,ek)(ek,ek) ek = (x,ek) ek = Pkx ▶
= Pk (Pkx) = Pk (x,ek) ek = (x,ek) Pek = (x,ek)(ek,ek) ek = (x,ek) ek = Pkx ▶
3°. PkPj = 0, (x ¹ j). ◀ PkPj x = Pk (Pj x) = Pk (x,ej) ej = (x,ej) Pkej = (x,ej) 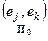 ek = 0 ▶
ek = 0 ▶
Для операторов - проекторов Pk имеем:
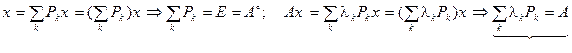 .
.
Такое представление эрмитового оператора А называется его спектральным разложением. Обратим еще внимание: 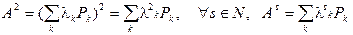 .
.
Def: Пусть Р (λ) – произвольный полином р й – степени, т.е. 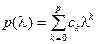 . Тогда определим полином от оператора слеующим образом:
. Тогда определим полином от оператора слеующим образом: 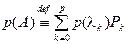 .
.
Тº. (Гамильтона-Кэли). Эрмитов оператор А является корнем своего
характеристического полинома: если 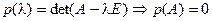 .
.
◀ 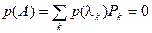 ▶
▶
 2015-05-05
2015-05-05 1042
1042








