Если функция f - это сумма n функций (основных элементарных или элементарных) f1, f2, …, fn, то есть, функция f задается формулой 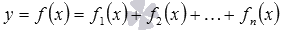 , то областью определения функции f является пересечение областей определения функций f1, f2, …, fn. Итак,
, то областью определения функции f является пересечение областей определения функций f1, f2, …, fn. Итак, 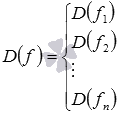 .
.
Пример.
Найдите область определения функции 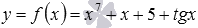 .
.
Решение.
Функция f представлена суммой четырех функций: f1 - степенной функции с показателем 7, f2 - степенной функцией с показателем 1, f3 - постоянной функцией и f4 - функцией тангенс.
Мы знаем, что 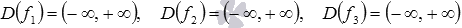 , а областью определения тангенса является множество всех действительных чисел, кроме чисел
, а областью определения тангенса является множество всех действительных чисел, кроме чисел 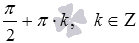 .
.
Область определения функции f – это пересечение областей определения функций f1, f2, f3 и f4, а это есть множество всех действительных чисел, за исключением чисел 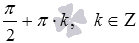 .
.
Ответ:
множество всех действительных чисел, кроме чисел 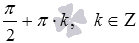 .
.
Пример.
Найдите область определения функции 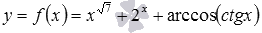 .
.
Решение.
В этом примере функция f есть сумма трех функций: f1 – степенная функция с показателем 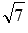 , f2 – показательной функции с основанием 2 и сложной функции f3, которой соответствует формула
, f2 – показательной функции с основанием 2 и сложной функции f3, которой соответствует формула 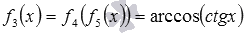 , где f4 – функция арккосинус, а f5 - котангенс.
, где f4 – функция арккосинус, а f5 - котангенс.
Областью определения функции f является пересечение множеств 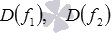 и
и 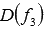 .
.
Так как нам известны области определения основных элементарных функций, то 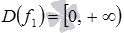 и
и 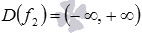 . Найдем область определения сложной функции f3:
. Найдем область определения сложной функции f3:
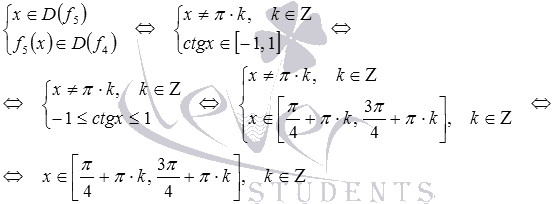
Теперь мы можем получить область определения исходной функции:
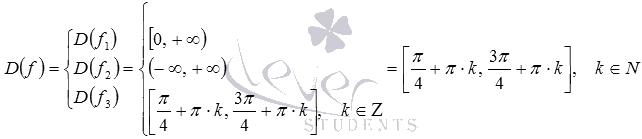
Ответ:
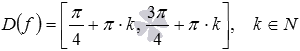 .
.
 2015-05-05
2015-05-05 2029
2029
