Под показательно-степенной функцией понимается функция, заданная формулой 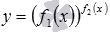 . По сути, показательно-степенная функция – это сложная функция вида
. По сути, показательно-степенная функция – это сложная функция вида 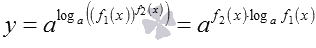 , где
, где 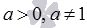 . Из этой записи хорошо видно, что область определения показательно-степенной функции находится из системы неравенств
. Из этой записи хорошо видно, что область определения показательно-степенной функции находится из системы неравенств 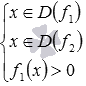 .
.
Пример.
Найдите область определения показательно-степенной функции 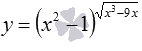 .
.
Решение.
Обозначим 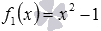 и
и 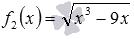 . Функция f1 - это целая рациональная функция, которая определена на множестве всех действительных чисел, то есть,
. Функция f1 - это целая рациональная функция, которая определена на множестве всех действительных чисел, то есть, 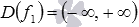 . Функция
. Функция 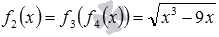 – сложная, f3 – функция квадратный корень,
– сложная, f3 – функция квадратный корень, 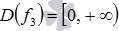 , а функция f4 – целая рациональная,
, а функция f4 – целая рациональная, 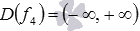 . Найдем область определения функции f2:
. Найдем область определения функции f2: 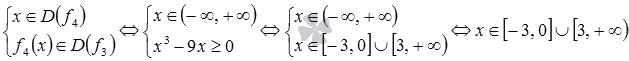 . Следовательно,
. Следовательно, 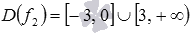 .
.
Осталось определить область определения исходной показательно-степенной функции, решив систему неравенств 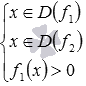 :
:
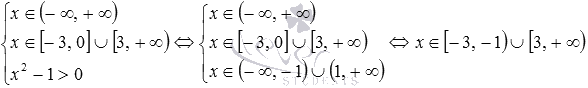
Ответ:
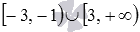 .
.
К началу страницы
В заключении отметим, что преобразования выражения, которое находится в правой части формулы, задающей функцию, нужно проводить очень аккуратно. Этим мы хотим сказать, что допустимы лишь тождественные преобразования, не влияющие на область определения исходной функции. Например, 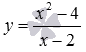 и
и 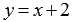 - это две разные функции, первая определена на множестве
- это две разные функции, первая определена на множестве 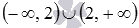 , а вторая – на множестве всех действительных чисел. Преобразование
, а вторая – на множестве всех действительных чисел. Преобразование 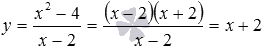 справедливо только тогда, когда
справедливо только тогда, когда 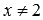 .
.
 2015-05-05
2015-05-05 2804
2804