Нахождение области определения дробных функций

Рассмотрим дробную функцию, заданную формулой 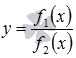. Чтобы найти область определения дробной функции перепишем ее в виде 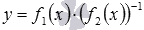. Имеем произведение двух функций: y=f₁(x) и сложной функции 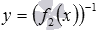. Область определения функции y=f₁(x) есть множество 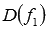, а область определения сложной функции 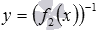определяется из системы .

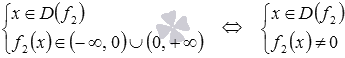Таким образом, область определения дробной функции 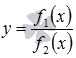находится из системы .

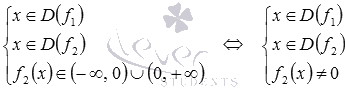Пример.

Найдите область определения функции .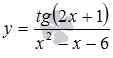

Решение.

Данная дробная функция представляет собой отношение двух функций: сложной функции 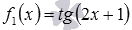и целой рациональной функции 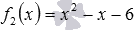, областью определения которой является множество всех действительных чисел. Тогда область определения функции 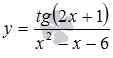находится из системы неравенств .

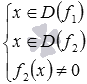В свою очередь сложную функцию 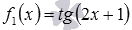представим как 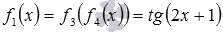, где f₃ – функция тангенс и ее область определения составляют все действительные числа, кроме чисел 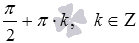, а f₄ – целая рациональная функция и 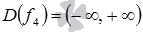. Теперь мы можем найти область определения функции f₁: .

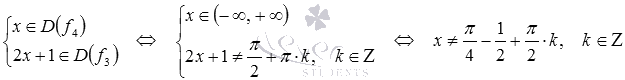Теперь можно приступать к отысканию требуемой области определения дробной функции :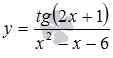

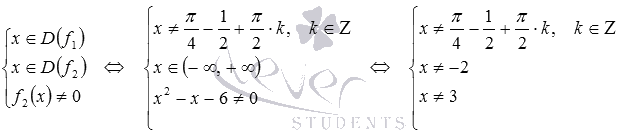
Ответ:

множество всех действительных чисел, кроме чисел -2, 3 и .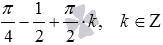

Нахождение области определения функции, содержащей аргумент под знаком логарифма и в основании логарифма, сводится к нахождению области определения дробной функции.

Действительно, функция 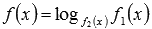есть функция 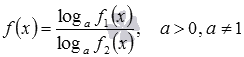. Так как областью определения логарифмической функции с основанием a является множество действительных положительных чисел, то области определения сложных функци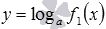й и 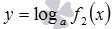определяются из систем 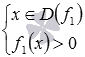и 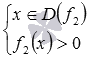соответственно. Тогда область определения дробной функции 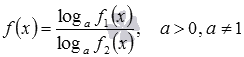, а значит и функции 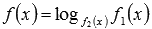, находится из системы неравенств вида .

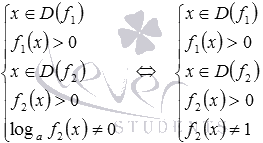Пример.

Найдите область определения функции .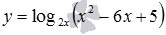

Решение.

Обозначим 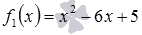и 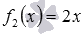. f₁ и f₂ – целые рациональные функции, поэтому, 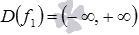и 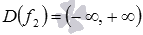. Мы выяснили, что область определения функции 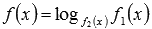находится из системы неравенств 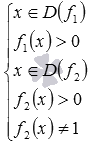. Подставляем в нее наши данные и находим ее решение:

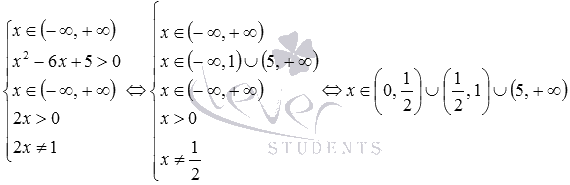
Таким образом, областью определения исходной функции является множество .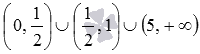

Ответ:

.

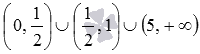К началу страницы