2015-05-06
983
Пусть суммарное гармоническое и постоянное напряжение вида (7) подаётся на вход электрической цепи с НЭ, характеристика которого аппроксимирована кусочно-линейной линией и описывается формулой (5). В этом случае временнáя диаграмма тока, протекающего через нелинейные цепи, имеет форму косинусоидальных импульсов с отсечкой их нижней части (рис.5).
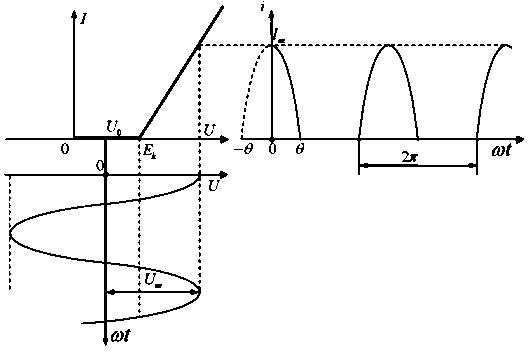
Рис.5. Форма тока при кусочно-линейной аппроксимации
характеристики НЭ
Параметр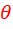 
(в радианах или градусах), при котором ток изменяется от максимального значения 
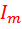до нуля, называется углом отсечки.
(Другое определение этого параметра: угол, соответствующий половине той части периода, в течение которой в выходной цепи нелинейного элемента протекает ток, называется углом отсечки и обозначается буквой q).
Изменение фазы, соответствующее длительности полного импульса на выходе цепи, равно 
. Из графиков рис.5 можно определить, что при фазовом угле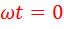 
напряжение начала характеристики
,
откуда
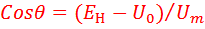........................ (11)
Подставив в формулу (5) суммарное напряжение источников сигнала и смещения из выражения (7) и напряжение начала характеристики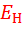 
получим аналитическую запись формы тока в зависимости от фазового угла:
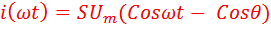, при условии 
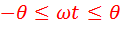....... (12)
Полученную чётную функцию 
периодической последовательности импульсов тока (12) можно разложить в тригонометрический ряд Фурье (8), в котором период повторения составляет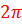 
, длительность импульса - 
, а текущей переменной является мгновенный фазовый угол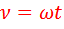 
.
В этих импульсах тока постоянная составляющая запишется следующим образом:
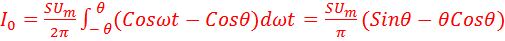........ (13)
Амплитуда первой гармоники
.....
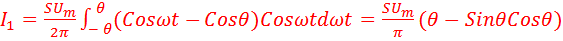.... (14)
Подобным же образом определяются амплитуды гармонических составляющих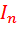 
и для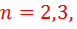 
..... При этом обобщённая формула для вычисления этих гармоник будет:
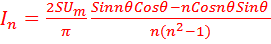................. (15)
В радиотехнике полученные результаты записываются в специальной форме:
; 
;..... 
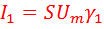....... (16)
Здесь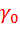 
, 
,......, 
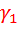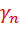– так называемые функции (коэффициенты)Берга, или коэффициенты гармоник, отражающие величины присутствующих гармоник в спектре преобразованного тока, которые аналитически записываются следующим образом:
,
,
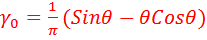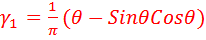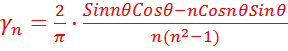,............ (17)
где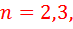 
......
Пример 2. Характеристика нелинейного элемента имеет кусочно-линейную аппроксимацию двумя отрезками, у которой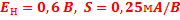 
. На элемент воздействует суммарное (постоянное и переменное) напряжение 
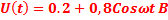. Определить постоянную составляющую и первую гармонику тока, протекающих через нелинейный элемент цепи.
Решение. Воспользовавшись формулой (11), находим, что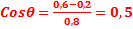 
. Отсюда угол отсечки тока, протекающего через нелинейный элемент, 
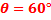. Два первых коэффициента гармоник, соответствующих этому углу, будут: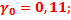 
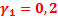. Подставив последовательно эти значения в соотношение (16), вычисляем соответственно амплитуды постоянной составляющей и первой гармоники: 
, 
.
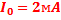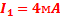Коэффициенты гармоник очень часто используются в инженерных расчётах, например, при проектировании схем нелинейных усилителей мощности, умножителей частоты и автогенераторов. Поэтому они приводятся в специальной литературе.
Нелинейное усиление мощности и умножение частоты
В различных устройствах радиоэлектроники (особенно в радиопередающих устройствах) широкое применение находят резонансные усилители мощности и умножители частоты. Обычно транзисторный резонансный усилитель работает в линейном режиме (усилительный элемент работает в режиме «А») и поэтому имеет КПД менее 50%. Эффективный способ повышения энергетических показателей резонансного усилителя мощности – использование заведомо нелинейного режима работы его активного элемента (режим с отсечкой выходного тока, режим «С»). Необходимым условием работы таких схем является сохранение формы усиливаемого сигнала с минимальными нелинейными искажениями.
