2015-05-06
1876
При амплитудной модуляции (AM) амплитуда несущего синусоидального колебания подвергается воздействию модулирующей функции (рис. 1.46).
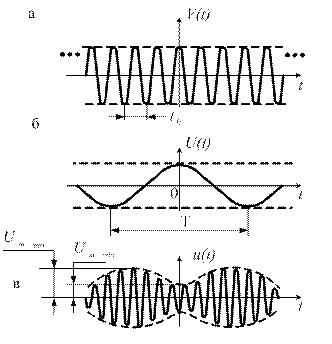
Рис. 1.46
Аналитическое выражение несущего колебания имеет вид:
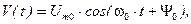где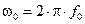 
, 
.
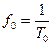Аналитическое выражение модулирующего колебания определяется выражением:
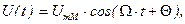где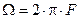 
, 
.
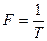Мгновенное значение радиосигнала с однотональной AM определяется выражением:
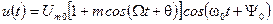, где:
;
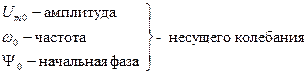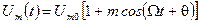– "переменная амплитуда";
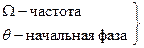– модулирующий функции;
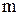– коэффициент модуляции или коэффициент глубины модуляции,
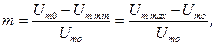
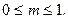
Для определения спектра однотонального АМ сигнала проведем тригонометрические преобразования:
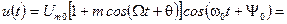
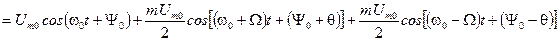
Как видно из приведенного выражения спектр сигнала состоит из трех составляющих: одной – с частотой несущего колебания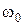 
и двух других – с частотам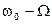и 
и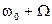 
.
Графики АЧС и ФЧС приведены на рисунке 1.47. Сравнивая полученный спектр со спектром несущего колебания, заметим, что модуляция приводит к появлению двух новых колебаний с боковыми частотами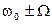 
.
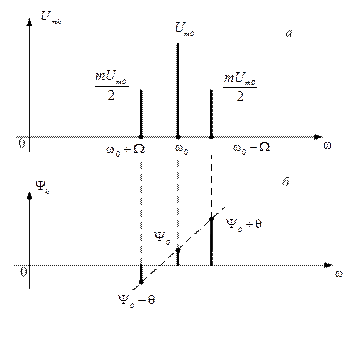
Рис. 1.47
Амплитуды этих колебаний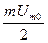 
зависят от коэффициента модуляции .
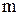Выражения для мгновенного значения амплитудно-модулированного сигнала при модуляции несколькими частотами имеет вид
.
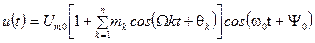Выполняя аналогичные тригонометрические преобразования получим спектр этого сигнала
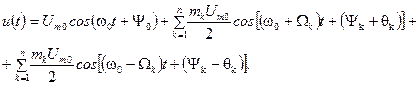
Амплитудно-частотный спектр этого колебания изображен на рисунке 1.48
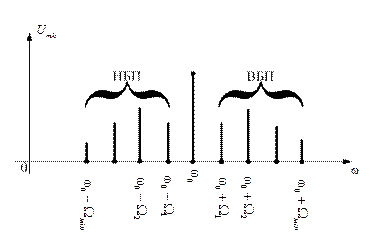
Рис. 1.48
Он состоит из несущего колебания и составляющих нижней и верхней боковых полос спектра.
