Отраженные коды

Отличительной особенностью отраженных кодов является то, что соседние кодовые комбинации различаются цифрой только в одном разряде. В этих кодах нет одновременного изменения цифр в нескольких разрядах.

Наибольшее распространение из всех отраженных кодов получил код Грея.Рассмотрим особенности кода Грея на примере.

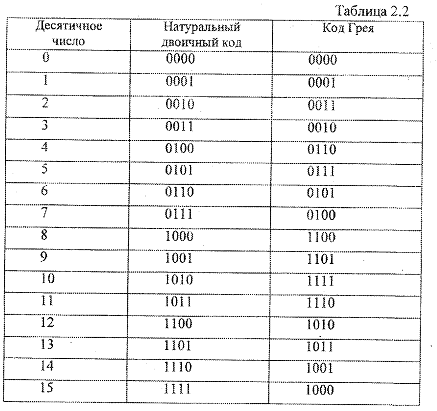
Таблица позволяет установить ряд характерных особенностей кода Грея:

Каждая последующая комбинация всегда отличается от предыдущей только в одной позиции (одном разряде).

Смена значений элементов в каждом разряде при переходе от комбинаций к комбинации происходит вдвое реже, чем в простом коде.

В коде Грея можно выделить оси симметрии (оси «отражения»), относительно которых наблюдается идентичность элементов в некоторых разрядах. Имеет место симметрия относительно оси, проведенной между числами 7 и 8. В комбинациях, симметричных относительно этой оси, идентичны три символа младших разрядов.

Ось симметрии, которая проходит в n–значном коде Грея между комбинациями соответствующим уровням (числам) s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 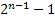и 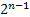называется главной осью симметрии.

По сравнению с простым кодом код Грея позволяет уменьшить ошибки неоднозначности считывания, а также ошибки, вызванные помехами при передаче информации по каналам связи. Недостатком кода Грея и других отраженных кодов является их «невесомость», т.е. в них вес единицы не определяется номером разряда.

Правила перевода простого двоичного кода в код Грея:

1. Под двоичным числом записать тоже число со сдвигом вправо на один разряд (младший разряд сдвигаемого числа теряется)

2. Произвести поразрядное сложение сдвинутого и несдвинутого чисел по модулю 2.

Правила перевода кода Грея в простой двоичный код:

1. Цифра старшего разряда остается без изменения.

2. Каждая последующая цифра инвертируется столько раз сколько единиц ей предшествует.