2015-05-06
3171
Дифференциальные уравнения для пограничного слоя выводятся из уравнений Навье-Стокса. Впервые они были получены Л. Прандтлем в 1904 году для течений, происходящих с большими числами Рейнольдса.
В уравнениях Навье-Стокса[13], записанных для плоского потока несжимаемой жидкости при отсутствии массовых сил (X=Y=0),
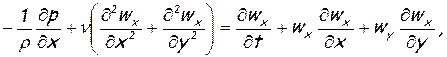(6.44)
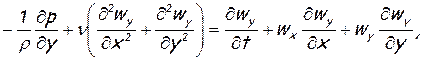(6.45)
а также в уравнении неразрывности
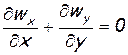(6.46)
Прандтлем была сделана оценка порядка величин входящих в них членов. Было установлено, что при достаточно высоких числах Рейнольдса величины
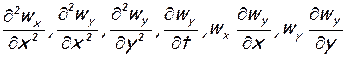
в пограничном слое имеют высший порядок малости, по сравнению с остальными[14]. Поэтому они могут быть отброшены. Уравнение (6.45) приобретает вид ∂р/∂у=0, из него вытекает уже упоминавшееся свойство неизменности статического давления в направлении поперек пограничного слоя. Уравнение (6.44) несколько упрощается, а (6.46) остается в том же виде. В результате система уравнений пограничного слоя принимает вид
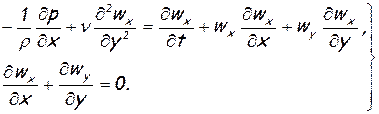(6.47)
Формулы (6.47) называют уравнениями Прандтля.
В качестве граничных условий при решении системы (6.47) берут следующие
|
|
|
wx = wy = 0 при y = 0 (на стенке),
wx = w (x, t) при y = ∞ (за пределами пограничного слоя).
Метод расчета пограничного слоя путем решения уравнений Прандтля является строгим. Однако для многих практических задач он оказывается настолько сложным и трудоёмким, что для быстрого получения результата приходится пользоваться приближенными методами.
Эффективным приближенным методом расчета является, в частности, метод, в котором используется интегральное уравнение импульсов, называемое также интегральным соотношением Кармана.
Рассмотрим это соотношение более подробно. На рисунке 118 изображен участок потока, длиной dх, в котором контрольной поверхностью АВЕF ограничен объем, находящийся в пограничном слое. Размер объема, измеренный перпендикулярно плоскости чертежа, принят равным единице.
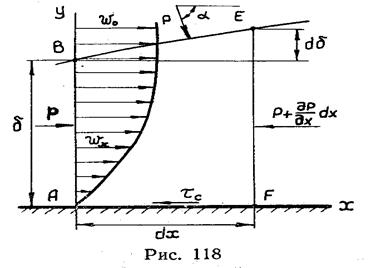
Согласно теореме Эйлера о количестве движения, равнодействующая всех сил, действующих на выделенный объем, должна равняться изменению количества движения жидкости, протекшей через контрольную поверхность, которая ограничивает этот объем. В проекции на ось х это запишется так:
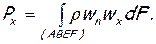(6.48)
(по двум другим осям изменения давления и количества движения не происходит).
Если положить, что массовые силы отсутствуют, то в число действующих сил, которые дают проекции на ось х, надо включить силы давления на поверхности АВ, ВЕ, ЕF и силы трения на поверхность АF [15]. Тогда
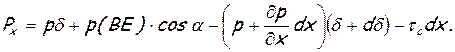
Раскрывая скобки, пренебрегая членами высших порядков малости и принимая во внимание, что (ВЕ)соs α = dδ, получим
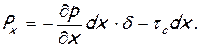(6.49)
Интеграл количества движения можно разбить по участкам, из которых составляется контрольная поверхность
|
|
|
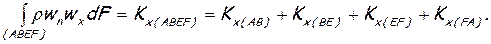(6.50)
Здесь индекс в скобках обозначает участок поверхности, через который протекает жидкость с соответствующим количеством движения. Очевидно, что Кх(FA)=0, так как через твердую стенку жидкость не протекает (wn=0). Остальные количества движения можно представить так:
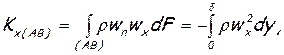(6.51)
так как wn = – wх,
Kх(BЕ)= – w0 mсек(ВЕ) ,
потому что скорость потока, входящего через ВЕ, постоянна и равна w0. Но
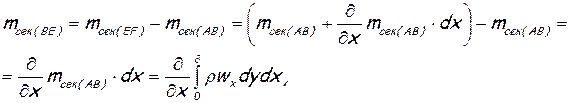
следовательно,
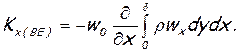(6.52)
Аналогично рассуждая, нетрудно установить, что
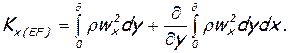(6.53)
Подставив величины, найденные из выражений (6.51), (6.52), (6.53) в формулу (6.50), а затем (6.50) и (6.49) в формулу (6.48), получим следующее уравнение:
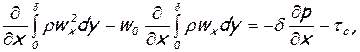(6.54)
называемое интегральным соотношением для пограничного слоя. Для несжимаемой жидкости плотность ρ выходит из под знаков интеграла и производной. Тогда
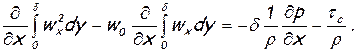(6.55)
Уравнения (6.54) и (6.55) пригодны для случаев обтекания как плоской, так и криволинейной поверхности.
