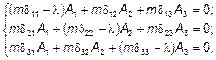
| или | 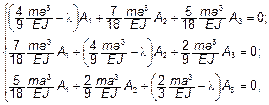
|
где l – собственные числа, связанные с собственными w частотами зависимостью 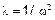 .
.
Упрощаем систему, умножая на 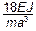 и вводя обозначение
и вводя обозначение 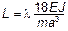 :
:
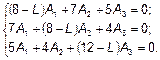 (1)
(1)
Это однородная система линейных алгебраических уравнений относительно амплитуд A 1, A 2, A 3. Она имеет ненулевое решение, если ее определитель равен нулю, т. е.
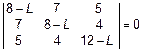 . (2)
. (2)
4 Характеристическое уравнение и его решение. Раскрыв определитель (2), получаем характеристическое уравнение
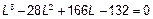 .
.
Решая это уравнение (например, на ЭВМ), находим корни:
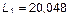 ;
; 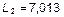 ;
; 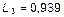 .
.
(Корни нумеруем так, чтобы выполнялось условие L 1 > L 2 > L 3).
5 Частоты колебаний. Частоты собственных колебаний 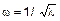 . С учетом обозначения L, введенного в (1), получаем
. С учетом обозначения L, введенного в (1), получаем
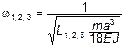 ;
; 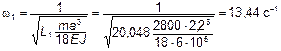 ;
;
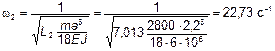 ;
;
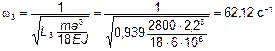 .
.
(Частоты должны быть пронумерованы так, чтобы w1 < w2 < w3).
6 Формы колебаний. Первая форма колебаний соответствует частоте 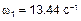 ,
, 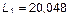 . В системе (1) к величинам L, A 1, A 2, A 3 добавляем индекс «1»:
. В системе (1) к величинам L, A 1, A 2, A 3 добавляем индекс «1»:
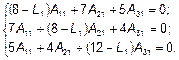 (3)
(3)
Задаемся значением А 11 = 1. Подставляем А 11 и L 1 в (3). Неизвестны всего две амплитуды А 21 и А 31, для определения которых можно использовать любые два уравнения системы (3), например, первое и второе:
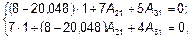
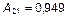 ;
; 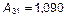 .
.
Вторая форма колебаний соответствует 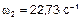 ,
, 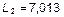 . В системе (1) к L, A 1, A 2, A 3 добавляем индекс «2»:
. В системе (1) к L, A 1, A 2, A 3 добавляем индекс «2»:
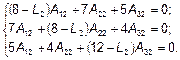 (4)
(4)
Задаемся значением А 22 = 1. Подставляем А 22 и L 2 в (4). Неизвестны всего две амплитуды А 12 и А 32, для определения которых можно использовать любые два уравнения системы (4), например, первое и второе:
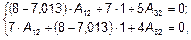
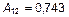 ;
; 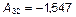 .
.
Третья форма колебаний соответствует 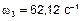 ,
, 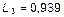 . В системе (1) к L, A 1, A 2, A 3 добавляем индекс «3»:
. В системе (1) к L, A 1, A 2, A 3 добавляем индекс «3»:
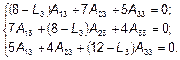 (5)
(5)
Задаемся значением А 33 = 1. Подставляем А 33 и L 3 в (5). Неизвестны всего две амплитуды А 13 и А 23, для определения которых можно использовать любые два уравнения системы (5), например, первое и второе:
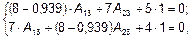
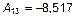 ;
; 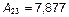 .
.
Смысл найденных величин: Аkm (k, m = 1, 2, 3) – амплитудное значение перемещения yk при колебаниях с частотой w m.
Показываем формы колебаний (рисунок 3). Положительные амплитуды откладываем в направлениях, совпадающих с направлениями перемещений y на рисунке 1, отрицательные – противоположно.
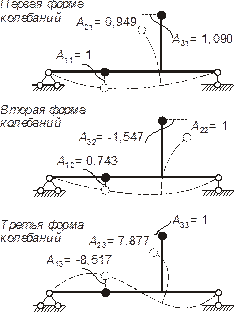
Рисунок 3
7 Проверка ортогональности форм колебаний. Для рассматриваемой системы с тремя степенями свободы, у которой массы точечных грузов одинаковы, должны выполняться условия
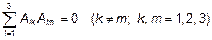 ;
;
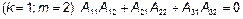 ;
;
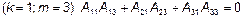 ;
;
 .
.
Подставляя значения амплитуд, получим
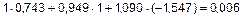 ;
;
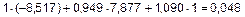 ;
;
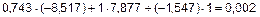 .
.
Погрешность не превышает 5 %, проверка выполняется.
Примечание. Расчеты, начиная с п. 3, можно выполнить на ЭВМ. Программа в среде MathCad приведена в приложении.
Приложение
| Èñõîäíûå äàííûå |
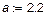
|
| (ì) |
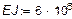
|
| (Í ì2) |
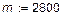
|
| (êã) |
| Ìàòðèöà ïîäàòëèâîñòè |
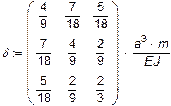
|
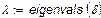
|
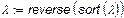
|
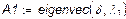
|
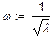
|
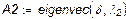
|
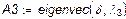
|
| Ðåçóëüòàòû |
| Cîáñòâåííûå ÷èñëà è ÷àñòîòû |
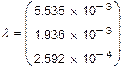
|
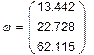
|
| (ñ-1) |
| Cîáñòâåííûå âåêòîðû |
| À 11 À 21 À 31 |
| À 12 À 22 À 32 |
| À 13 À 23 À 33 |
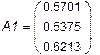
|
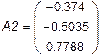
|
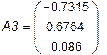
|
| Ïðîâåðêà |
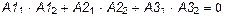
|
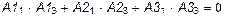
|
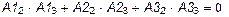
|
 2015-05-06
2015-05-06 229
229







