При решении задач о прохождении сигналов через электрические цепи основное внимание уделяют изменениям информационных параметров сигналов, поскольку это связано с проблемой сохранения информации, переносимой сигналами. В случаях, когда информация заложена непосредственно в форме сигнала (случай простых сигналов) задача сохранения информации сводится к задаче сохранения формы (или спектра) сигнала.
Иначе дело обстоит с радиосигналом, в котором информация заключена в одном из нескольких параметров высокочастотного колебания. Не обязательно сохранять полностью структуру этого колебания; достаточно лишь сохранить закон изменения того параметра, в котором заключена информация. Так, в случае амплитудно-модулированного колебания, важно передать огибающую амплитуд, а некоторое изменение частоты или несущее колебание, не имеющее существенного значения, при анализе можно не учитывать. При передаче радиосигналов с угловой модуляцией, наоборот, основное внимание следует уделить точному воспроизведению закона изменения частоты и фазы, а изменением амплитуды можно пренебречь.
Эти особенности радиосигналов открывают путь к некоторому упрощению методов анализа их передачи через линейные цепи. Возможность упрощения особенно существенна, когда радиосигнал представляет собой узкополосный процесс, а цепь - узкополосную систему. Это как раз и характерно для реальных радиосигналов и реальных радиоцепей.
а) Приближенный спектральный метод. Пусть цепь представляет собой избирательную систему, передаточная функция 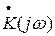 которой имеет максимум вблизи частот wp и (-wp). И пусть на ее входе действует высокочастотное модулированное колебание S(t) спектральная характеристика которого имеет два максимума вблизи частот w0 и (-w0). В общем случае резонансная частота цепи wp не совпадает с центральной частотой сигнала w0, т.е. имеет место расстройка
которой имеет максимум вблизи частот wp и (-wp). И пусть на ее входе действует высокочастотное модулированное колебание S(t) спектральная характеристика которого имеет два максимума вблизи частот w0 и (-w0). В общем случае резонансная частота цепи wp не совпадает с центральной частотой сигнала w0, т.е. имеет место расстройка
Dw=w0-wp (20)
которая является величиной того же порядка, что и полоса пропускания цепи.
Составим выражение для сигнала на выходе цепи. Если входной сигнал имеет гармоническое заполнение, т.е. S(t)=A(t)cos( w0 t+q(t)), то выкладки значительно упрощаются при использовании понятия аналитического сигнала:
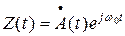 (21)
(21)
Спектральная функция этого сигнала 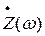 существует только в области положительных частот, поэтому при определении аналитического сигнала на выходе цепи следует исходить из выражения:
существует только в области положительных частот, поэтому при определении аналитического сигнала на выходе цепи следует исходить из выражения:
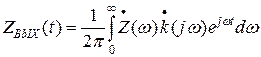 (22)
(22)
Спектральные функции высокочастотного модулированного колебания 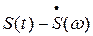 и аналитического сигнала
и аналитического сигнала 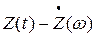 при w> 0 связаны соотношением
при w> 0 связаны соотношением 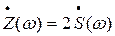 , причем при w> 0
, причем при w> 0 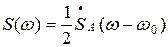 , где
, где 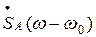 ‑спектральная функция огибающей.
‑спектральная функция огибающей.
Следовательно 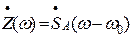 .
.
Подставляя это выражение в (22), получаем
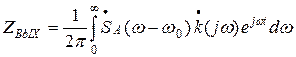 (23)
(23)
Введем переменную W=w-w0. Тогда
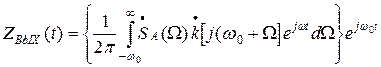 (24)
(24)
Из сопоставления (24) с (21) видно, что выражение, стоящее в фигурных скобках соответствует комплексной огибающей выходного колебания:
Дальнейшее упрощение анализа вытекает из свойств передаточной функции резонансных цепей, обладающих сильно выраженной частотной избирательностью: Модуль коэффициента передачи 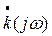 быстро убывает при удалении w от резонансной частоты. Поэтому передаточную функцию целесообразно выражать в виде функции расстройки частоты w относительно резонансной частоты wp:
быстро убывает при удалении w от резонансной частоты. Поэтому передаточную функцию целесообразно выражать в виде функции расстройки частоты w относительно резонансной частоты wp:

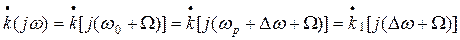 (26)
(26)
где постоянный параметр расстройки Dw=w0-wp. Т.к. при W=-w0 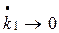 , нижний предел интегрирования в (25) можно заменить на -¥. При этом оно принимает вид:
, нижний предел интегрирования в (25) можно заменить на -¥. При этом оно принимает вид:
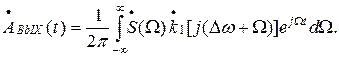 (27)
(27)
Это выражение ничем не отличается от обычного интеграла Фурье, определяющего оригинал по заданной спектральной плотности огибающей 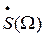 и передаточной функции
и передаточной функции 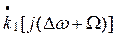 .
.
Заменив jW на p, получим выражение в форме обратного преобразования Лапласа:
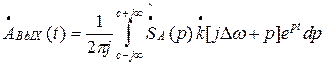 (28)
(28)
Таким образом, анализ передачи узкополосного высокочастотного колебания через избирательную цепь по существу сводится к анализу изменений, претерпеваемых комплексной огибающей входного сигнала. После нахождения Aвых(t) и qвых(t) для выходного аналитического сигнала можно будет написать следующее выражение:
Zвых(t)=Aвыхej[w0t+qвых(t)] (29)
откуда Sвых(t)=Aвых(t)cos[w0t+qвых(t)] (30)
Вычисления, связанные с определением 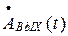 по формуле (28), значительно проще, чем при непосредственном определении Sвых(t) с помощью обратного преобразования Лапласа, так как переход от
по формуле (28), значительно проще, чем при непосредственном определении Sвых(t) с помощью обратного преобразования Лапласа, так как переход от 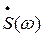 к
к 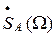 и от
и от 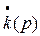 к
к 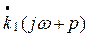 сокращает число особых точек подинтегральной функции.
сокращает число особых точек подинтегральной функции.
б) Упрощенный метод интеграла наложения. (Метод огибающей).
Упрощение спектрального метода было достигнуто упрощением передаточной функции избирательной цепи 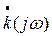 . Аналогично метод интеграла наложения можно упростить укорочением импульсной характеристики h(t), тесно связанной с передаточной функцией
. Аналогично метод интеграла наложения можно упростить укорочением импульсной характеристики h(t), тесно связанной с передаточной функцией 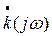 .
.
Основываясь на общем выражении
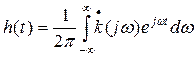
и переходя к аналитической функции Zh(t), соответствующей физической функции h(t), находим
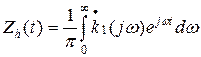 (31)
(31)
Заменим переменную w=w0+W. Тогда с учетом формулы (26) и после замены нижнего предела -w0 на -¥ получим
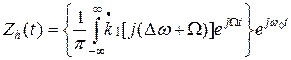
С другой стороны, представив искомую импульсную характеристику в виде узкополосной функции
h(t)=H(t)cos[w0t+gh(t)]
имеем:
Zh(t)=H(t)ej[w0t+gh(t)]=H(t)ejgh(t)ejw0t= 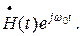 (33)
(33)
Из сравнения (32) и (33) непосредственно вытекает равенство, определяющее комплексную огибающую импульсной характеристики h(t):
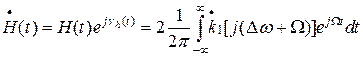 (34)
(34)
Применение этого выражения упрощает вычисление импульсной характеристики h(t).
Обратимся теперь к (27). Используя правило, согласно которому произведению двух спектров 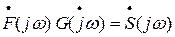 соответствует функция времени S(t), являющаяся сверткой функций f(t) и g(t):
соответствует функция времени S(t), являющаяся сверткой функций f(t) и g(t):
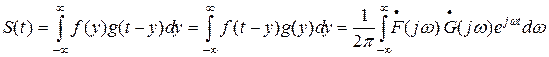 , (35)
, (35)
где y - временной интервал, в течении которого одновременно существуют функции f(t) и g(t), из (27) можем определить 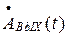 в виде свертки двух функций времени, соответствующих спектральным функциям
в виде свертки двух функций времени, соответствующих спектральным функциям 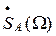 и
и 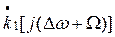 . Первой из этих функций соответствует
. Первой из этих функций соответствует 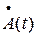 , а второй, как это следует из (34) -
, а второй, как это следует из (34) - 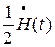 . Следовательно
. Следовательно
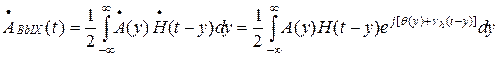 (36)
(36)
Это выражение является общим, пригодным для любых избирательных цепей и любых узкополосных сигналов. В тех случаях, когда свободные колебания характеризуются постоянной частотой заполнения, как, например, в одиночном колебательном контуре, gh(t) вырождается в постоянную фазу и выражение (36) существенно упрощается. То же самое относится и к сигналам с немодулированной частотой заполнения, когда q(t) обращается в постоянную величину.
Метод интеграла наложения эффективен в тех случаях, когда временные характеристики сигналов или цепей (или тех и других) оказываются более простыми, чем спектральные. Такое положение имеет место, например, при анализе прохождения ЧМ сигналов.
Л 14.
 2015-05-06
2015-05-06 991
991








