Электрическая цепь осуществляет преобразование сигналов, поступающих на ее вход. Поэтому в самом общем случае математическую модель цепи можно задать в виде соотношения между входным воздействием Sвх(t) и выходной реакцией Sвых(t):
Sвых(t)=TSвх(t),
где Т - оператор цепи.
На основании фундаментальных свойств оператора можно сделать заключение о наиболее существенных свойствах цепей.
1. Если оператор цепи Т не зависит от амплитуды воздействия, то цепь называется линейной. Для такой цепи справедлив принцип суперпозиции, отражающей независимость действия нескольких входных воздействий:
T[Sвх1(t)+ Sвх2(t)+...+ Sвхn(t)]=TSвх1(t)+TSвх2(t)+...+TSвхn(t) (1)
Очевидно, что при линейном преобразовании сигналов в спектре отклика нет колебаний с частотами, отличными от частот спектра воздействий.
Класс линейных цепей образуют как пассивные цепи, состоящие из разисторов, конденсаторов, индуктивностей, так и активные цепи, включающие еще и транзисторы, лампы и т.п. Но в любой комбинации этих элементов их параметры не должны зависеть от амплитуды воздействия.
2. Если сдвиг входного сигнала во времени приводит к такому же сдвигу выходного сигнала, т.е.
Sвых(t 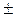 t0)=TSвх(t
t0)=TSвх(t 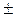 t0), (2)
t0), (2)
то цепь называют стационарной. Свойство стационарности не распространяется на цепи, содержащие элементы с переменными во времени параметрами (индуктивности, конденсаторы и т.п.).
2.2. Дельта - функция - как пример пробного сигнала.
Для анализа прохождения сигналов через электрические цели широко используются пробные сигналы, обладающие какими - либо характерными свойствами. Такой функцией, в частности, является дельта-функция d(t), обращающаяся в ноль при t¹0 и в бесконечность при t=0, так, что
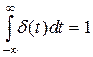 (3).
(3).
Этому определению удовлетворяет, например, прямоугольный импульс длительностью tu , амплитуда которого обратно пропорциональна его длительности 1/tu . При tu® 0 амплитуда импульса бесконечно растет, а площадь остается постоянной - равной единице. Действительно, если
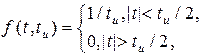
то дельта-функцию можно определить как d(t)= 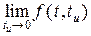
При этом
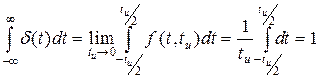
В более общем случае дельта-функцию можно записать в виде
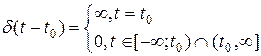 (4)
(4)
Спектральную плотность дельта-импульса A d(t) найдем с помощью прямого преобразования Фурье:
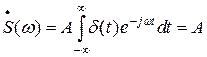 (5)
(5)
На основании определения дельта-функции интервал интегрирования в формуле (5) можно сделать сколь угодно малым, лишь бы он включал в себя момент t=0. В пределе он может быть устремлен к нулю и подъинтегральная функция ejwt примет значение, равное единице. Таким образом 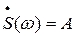 . Следовательно, спектральная плотность дельта-импульса имеет равномерный частотный спектр. ФЧХ дельта-импульса равна нулю для всех частот. Это означает, что все гармонические составляющие начинаются с одной фазы и образуют бесконечный пик при t=0.
. Следовательно, спектральная плотность дельта-импульса имеет равномерный частотный спектр. ФЧХ дельта-импульса равна нулю для всех частот. Это означает, что все гармонические составляющие начинаются с одной фазы и образуют бесконечный пик при t=0.
По определению, дельта-функция обладает свойством, которое может быть выражено соотношением
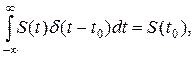 (6)
(6)
Его называют фильтрующим свойством дельта-функции, согласно которому интеграл от произведения произвольной функции на d(t-t0) равен значению этой функции в точке t=t0 .
На основании обратного преобразования Фурье выразим дельта-функцию через ее спектр:
d(t)= 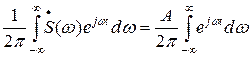 (7)
(7)
По аналогии с (7) можно ввести дельта-функцию аргумента w
d(w)= 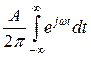 (8)
(8)
В (8) знак показателя экспоненты не влияет на значение интеграла, поскольку 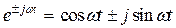 и независимо от знака интеграл от нечетной функции sin на симметричном интервале интегрирования равен нулю. Поэтому можно записать
и независимо от знака интеграл от нечетной функции sin на симметричном интервале интегрирования равен нулю. Поэтому можно записать
d(w)= 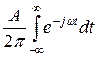 (9)
(9)
 2015-05-06
2015-05-06 347
347








