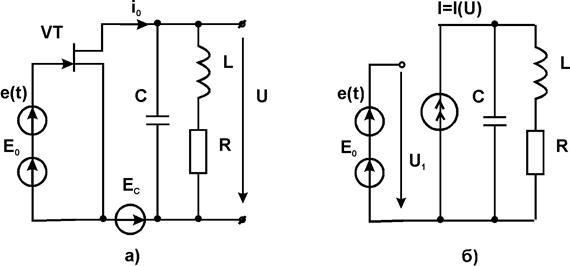
Умножение частоты

Умножение частоты осуществляют преобразование вида: Acosw₀t®Bcosnw₀t. Такие устройства представляют собой соединение нелинейного элемента и полосового фильтра, настроенного в резонанс на частоту выделяемой гармоники. Могут быть построены, например, на базе

резонансного усилителя, работающего в режиме с отсечкой тока стока (см. рис.)

Пусть 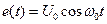. Найдем сначала ток i₀(t). Допустим, что нелинейная характеристика полевого транзистора описывается квадратичным полиномом

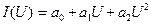
Тогда

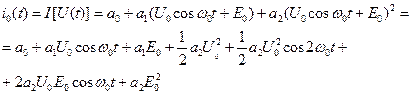
Выберем E₀ так, чтобы в отсутствии входного переменного сигнала ток был равен нулю, т. е. чтобы

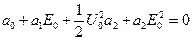
Тогда при действии переменного напряжения ток будет равен:

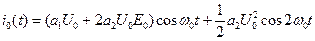
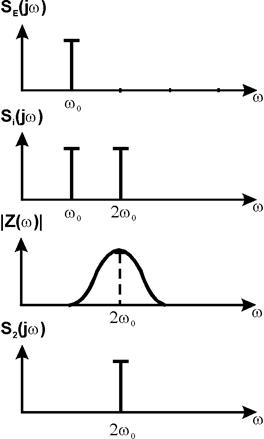
Рассмотрим спектры входного сигнала e(t) и ток i₀(t), последний состоит из двух гармоник. Падение напряжения на контуре, как на любом линейном двухполюснике, может быть рассчитано в частотной области:

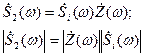
Сопротивление параллельного RLC контура описывается соотношением:

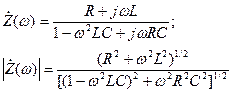
Зависимость 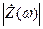при малых отклонениях R/L, т.е. при большой добротности 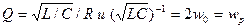имеет явно выражений избирательной характер (см. рис.). Так для частоты w₀ имеем 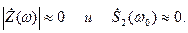На резонансной частоте w_p=2w₀ получаем

,

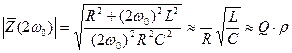где 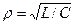- характеристическое сопротивление. Следовательно спектр выходного сигнала будет содержать одну гармонику с частотой 2w₀:

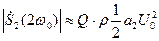
Если требуется умножение частоты на 3, т.е. n=3, то необходимо иметь нелинейность I(U) не ниже многочлена 3-го порядка и настраивать RLC-контур на частоту 3w₀. Аналогично для умножения на n требуется порядок нелинейности не ниже n.

5.4. Амплитудная модуляция

Амплитудные модуляторы производят преобразования вида 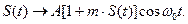Процесс амплитудной модуляции состоит в преобразовании “ медленного” сигнала S(t), называемого модулирующим, в быстро осциллирующий сигнал, амплитуда которого меняется по закону S(t):

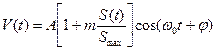
Здесь Acosw₀t - функция, называемая несущим колебанием, m - коэффициент модуляции (m≤1), где 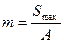; S_max=max|S(t), где S(t) – информационная функция.

(5)

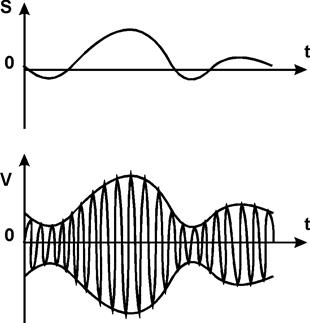
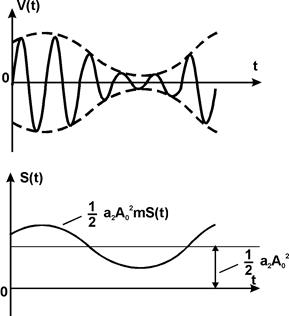
Например, если S(t) - сигнал вида (см. рис.), то соответствующий ему АМ-сигнал имеет вид следующего графика (см. рис.).

Определим спектр амплитудно-модулированного колебания.

Пусть АМ-колебание описывается функцией V(t)=f(t)cosw₀t. На основании прямого преобразования Фурье спектр этой функции будет содержать 2 группы гармоник: суммарной и разностной частот

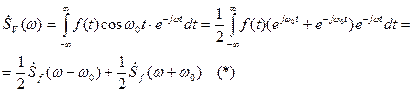
Поскольку по определению в выражении 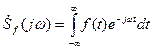есть спектр функции 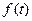, то формула (*) означает, что при АМ-модуляции спектр НЧ колебания переносится в область ВЧ колебания и раздваивается.

В нашем случа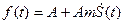е , где 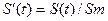. Спектр такой функции состоит из двух частей: 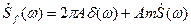(**). Следовательно, на основании формулы (*), спектр АМ-колебания будет иметь вид:

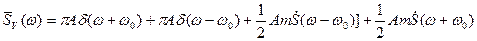
На рис. Изображены спектры модулирующего сигнала, несущего и АМ-колебания. Как видно, в результате модуляции спектр информационного сигнала переносится в область несущего колебания.

Процесс амплитудной модуляции является типичным преобразованием спектра сигнала S(t) и может быть осуществлен только в цепи с нелинейным элементом. Поскольку получение АМ-колебания требует двух сигналов: модулирующего S(t) и несущего Acosw₀t, на нелинейный элемент должна действовать сумма этих сигналов.

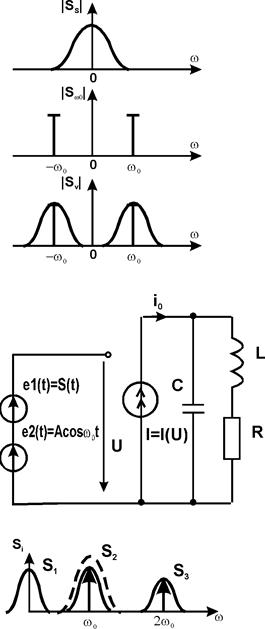
Включенный последовательно с нелинейным элементом линейный полосовой фильтр (ПФ) – например колебательный контур, настроенный на несущую частоту w₀, - выделяет полосу частот, соответствующую АМ-колебанию (см. рис.).

Проанализируем эту модель.

Пусть ВАХ безынерционного нелинейного элемента описывается многочленом второй степени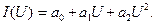

Определим входной ток полосового фильтра:

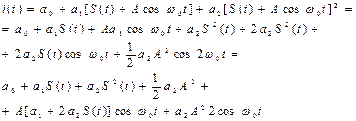
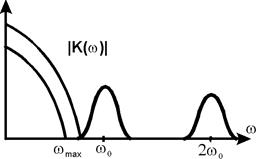
Рассмотрим спектральный состав тока, пологая что резонансная частота контура w₀ можно больше максимальной частоты w_max в спектре S(t) (см. пред. рис.). На этом рис. НЧ спектр S₁ обусловлен постоянной составляющей 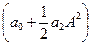и членами с S(t) и S²(t), а спектры S₂ и S₃ образуются сигналами, пропорциональными cosw₀t и cos2w₀t, соответственно. Если теперь принять, что полоса пропускания полосового фильтра сосредоточена вблизи w₀ (пунктир на графике), то он будет выделять колебание, пропорциональное cosw₀t, которое и представляет собой АМ-колебание.

Таким образом АМ-колебания получаются путем нелинейного сложения сигнала модуляции S(t) и несущего колебания. В результате получается выходное напряжение следующего вида.

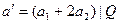
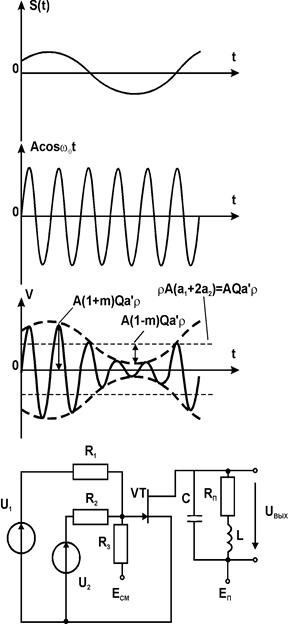
Практической схемой, осуществляющей процесс АМ-модуляции, является например следующая схема на полевом транзисторе и предварительным сложением модулирующего и несущего колебаний.

Напряжение между затвором и источником U_ЗИ вычисляется по формуле, полученной на основании законов Кирхгофа в предположении, что :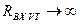

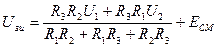
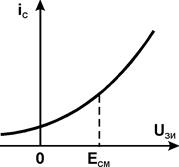
Подбором значений сопротивлений R₁, R₂, R₃ и напряжения смещения Е_СМ осуществляется выбор рабочей точки на передаточной характеристике транзистора (см. рис. 2). Наилучшим считается такое положение рабочей точки, когда коэффициенты разложения ВАХ в окружности этой точки обеспечивают максимальное значение коэффициента модуляции по первой гармонике выходного тока.

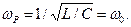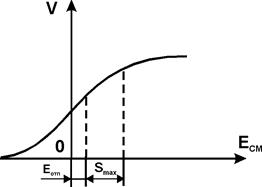
Модулированный сигнал получается как падение напряжение на колебательном контуре, параметры должны обеспечивать центральную частоту Сопротивление потерь R_П должно быть таким, чтобы добротность 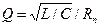цепи была достаточно большой, такой, чтобы полоса пропускания контура 2Dw << w₀ (несущей частоты). С другой стороны, спектр модуляционного сигнала не должен искажаться, должно W_m < Dw, где 2W_m - ширина спектра модуляционного колебания. Используя равенство 2Dw = w₀/Q, получаем неравенства для выбора параметров колебательного контура L, C, R_П:

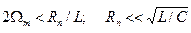
Коэффициенты а₀, а₁, а₂,..., определяющие вид нелинейной характеристики транзистора, зависят от выбора постоянного смещения на затворе, задаваемого сопротивлением R₁, R₂, R₃ E_cм. При изменении этого напряжения будет меняться амплитуда а₁АQ выходного напряжения V(t). Зависимость амплитуды первой гармоники тока на выходе нелинейного элемента (или падение напряжения на колебательном контуре на первой гармонике) от поданного напряжения смещения, называют статической модуляционной характеристикой (см. рис.). Величину E_ОПТ, оптимальную для рабочего модулятора, выбирают в середине линейного участка статической модуляционной характеристики. Амплитуда сигнала S_max не должна выходить за пределы линейного участка модуляционной характеристики. Статическая модуляционная характеристика – это не проходная ВАХ транзистора.

5.5. Детектирование АМ-колебаний

Процесс, обратной модуляции, называется демодуляцией или детектированием. При детектировании по колебанию 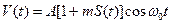необходимо восстановить сигнал S(t). Устройство, реализующее эту операцию, называют амплитудным демодулятором или детектором. При детектировании следует преобразовать сигнал V(t) так, чтобы потом можно было выделить сигнал S(t). Такое преобразование можно осуществить с помощью безынерционного нелинейного четырехполюсника с последующей низкочастной фильтрацией (см. рис.).

Предположим, что ВАХ БНЧ описывается квадратичной параболой:

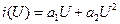
Тогда

или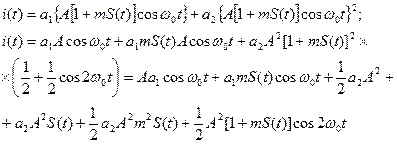

Как видно в спектре этого тока присутствует полезная составляю-щая тока S(t), которая может быть выделена фильтром нижних частот. На рис. приведен спектральный состав тока при условии, что в спектре сигнала S(t) максимальная частота w_max<<w₀. В полосу пропускания ФНЧ могут попасть составляющие, пропорциональные S²(t) (пунктир на рис.). Однако при малых m ими можно пренебречь.

Фильтр нижних частот отфильтровывает все высшие частоты в спектре тока и на его выходе имеется сигнал, пропорциональный S(t) с точностью до постоянной составляющей (см. рис.). Постоянная составляющая может быть легко отфильтрована последовательным включением емкости на выходе ФНЧ.

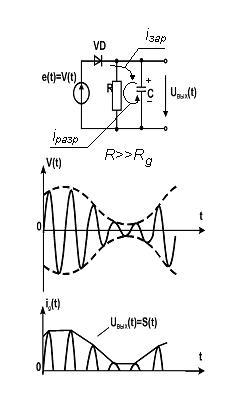
Простейшей критической схемой АМ-детектора может служить диодный детектор (см. рис.). Здесь в качестве ФНЧ используется RC - цепь. Токи всех высших гармоник протекают через емкость, не создавая сколько-нибудь заметного падения напряжения на ней, и U_ВЫХ(t) будет пропорционально S(t) (см. след. рис.). Заметим, что не всякий нелинейный элемент пригоден для детектирования, например, нельзя использовать только нечетные нелинейности (почему? - самостоятельно).

Л. 25-27

6. Анализ параметрических цепей

5.1. Общие понятия о параметрических цепях

Электрические системы, в которых хотя бы один из параметров (R, L или C) является переменным во времени, называется цепями с переменными параметрами, называется цепями с переменными параметрами, или параметрическими цепями. Если параметры зависят только от времени и не зависит от режима работы (т.е. т i или U), система является линейной.

С помощью параметрических систем, в которых переменным является активное сопротивление, могут осуществляться, например, такие преобразования сигналов: детектирование, выпрямление, амплитудная модуляция, преобразование частоты и др.

В цепях с переменными реактивными элементами, способными запасать и отдавать энергию, при определенных условиях могут происходить усиление и генерация колебаний. Это связано с появлением в системе отрицательного сопротивления, описывающего формально физический процесс внесения энергии в колебательную систему за счет работы сил, изменяющих параметр. Появление отрицательного сопротивления свидетельствует о наличии параметрической регенерации колебаний данной частоты. Под регенерацией понимается процесс частотного восполнения (восстановления) теряемой в системе энергии.

Математическое описание процессов, происходящих в параметрических цепях, сводится к линейным алгебраическим или дифференциальным уравнением с переменными (во времени) коэффициентами. В силу линейности цепей, связь между входными и выходными сигналами в них определяется с помощью импульсной характеристики g(t) (метод интеграла наложения) или с помощью комплексной передаточной функции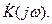

6.2. Импульсная характеристика и передаточная функция параметрической цепи

Для определения импульсной характеристики g(t, t), где t - время воздействия, t - время появления и действия отклика, непосредственно по заданным параметрам цепи необходимо использовать дифференциальное уравнение цепи.

Чтобы проанализировать методику нахождения g(t, t), рассмотрим простую цепь, описываемую уравнением первого порядка

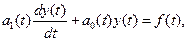(1)

где f(t) - воздействие, y(t) - отклик.

По определению импульсная характеристика является откликом цепи на одиночный дельта-импульс d(t-t), подаваемый на вход в момент t=t. Из этого определения следует, что если в правой части уравнения (1) положить f(t)= d(t-t), то в левой части можно принять y(t)= =d(t,t).

Таким образом приходим к уравнению

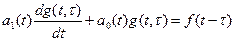(2)

Т.к. правая часть (2) равна нулю всюду, кроме точки t=t, функцию g(t) можно искать в виде решения однородного дифференциального уравнения

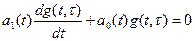(3)

при начальных условиях, вытекающих из уравнения (2), а также из условия, что к моменту приложения импульса d(t-t) в цепи отсутствуют токи и напряжения.

В уравнении (3) переменные разделяются:

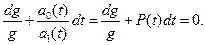
Откуда

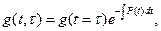(4)

где 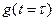- значения импульсной характеристики в момент воздействия.

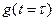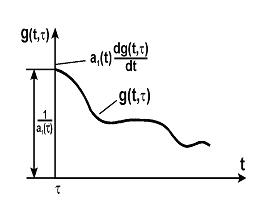
Для определения начального значения вернемся к исходному уравнению (2). Из него следует, что в точке 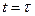функция g(t) должна совершить скачок на величину 1/а₁(х), (см. рис.), поскольку только при этом условии первое слагаемое в уравнении (2), a₁(t)[dg/dt], может образовывать дельта-функцию d(t-t).

Т.к. при 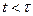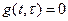, то в момент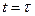

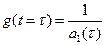Импульсная характериситка по уравнению (2)

(5)

Заменяя в (4) неопределенный интеграл определенным с переменным верхним пределом интегрирования, получаем соотношения для определения импульсной характеристики:

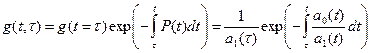(6)

Зная импульсную характеристику, нетрудно определить передаточную функцию линейной параметрической цепи, поскольку обе оси связаны парой преобразования Фурье:

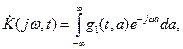(7)

где a=t-t - задержка сигнала. Функция g₁(t,a) получается из функции 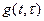заменой t=t-a.

Наряду с выражением (7) можно получить еще одно определение передаточной функции, в котором импульсная характеристика g₁(t,a) не фигурирует. Для этого используем обратное преобразование Фурье для отклика S_ВЫХ(t):

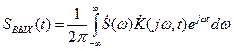(8)

Для случая, когда входной сигнал является гармоническим колебанием S(t)=cosw₀t. Соответствующий S(t) аналитический сигнал есть .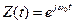

Спектральная плоскость этого сигнала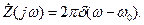

Подставляя 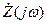вместо 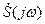в формулу (8), получаем:

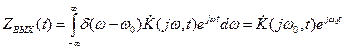
Отсюда находим

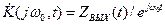(9)

Здесь Z_ВЫХ(t) - аналитический сигнал, соответствующий выходному сигналу S_ВЫХ(t).

Таким образом, выходной сигнал при гармоническом воздействии

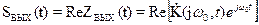(10)

определяется также, как и для любых других линейных цепей.

Если передаточная функция K(jw₀,t) изменяется во времени по передаточному закону с основной частотой W, то ее можно представить в виде ряда Фурье

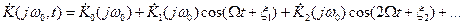(11)

где 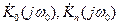- не зависящие от времени коэффициенты, в общем случае комплексные, которые можно трактовать как передаточные функции некоторых четырехполюсников с постоянными параметрами. Произведение 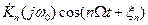можно рассматривать как передаточную функцию каскадного (последовательного) соединения двух четырехполюсников: одного с передаточной функцией 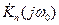, не зависящей от времени, и второго с передаточной функцией 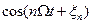, изменяющейся во времени, но не зависящей от частоты w₀ входного сигнала.

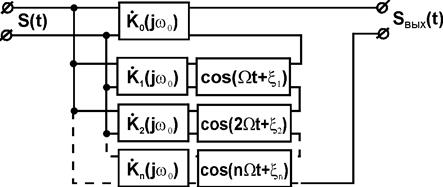Основываясь на выражении (11), любую параметрическую цепь с периодически изменяющимися параметрами можно представить в виде следующей эквивалентной схемы:

Откуда понятен процесс образования новых частот в спектре выходного сигнала

В соответствии с (9) аналитическй сигнал на входе будет равен

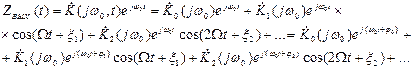(12)

здесь j₀, j₁, j₂ ...- фазовые характеристики четырехполюсников .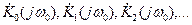

Переходя к вещественному сигналу на выходе, получаем

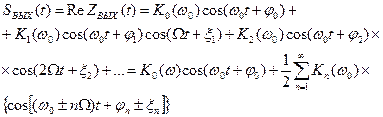(13)

Этот результат указывает на следующее свойство цепи с переменными параметрами: при изменении передаточной функции по любому сложному, по периодическому закону с основной частотой W гармонический выходной сигнал с частотой w₀ образует на выходе цепи спектр, содержащий частоты w, w₀±W, w₀±2W и т.д.

Если на входе цепи подается сложный сигнал, то все сказанное выше относится к каждой из частот w и входного спектра. Разумеется, что в линейной параметрической цепи никакого взаимодействия между отдельными компонентами входного спектра не существует (принцип суперпозиции), и на входа цепи не возникает частот вида nw₁± mw₂, где w₁ и w₂ - различные частоты входного сигнала.

6.3. Энергетика цепей с параметрическими реактивными элементами

Рассмотрим процессы, происходящие в цепи, содержащей конденсатор, емкость которого является функцией приложенного напряжения. Как элемент радиотехнических цепей параметрических конденсаторов не существует. В качестве параметрического конденсатора обычно применяются нелинейные конденсаторы. Модель параметрического конденсатора получается из модели нелинейного конденсатора путем замены С(U) на С(t). Рассмотрим как это реализуется. Пусть на нелинейный конденсатор подано колебание высокой частоты U_НК(t), амплитуда которого достаточна для того, чтобы вызвать заметную модуляцию емкости в соответствии с законом C(U). Будем называть это модулирующее колебание колебанием накачки и будем считать, что оно гармоническое, т.е. U_НК(t)= =U_mНКcos(w_НКt+j_НК). Найдем закон изменения емкости от времени, т.е. зависимость C(t).

Вольт-кулонную характеристику нелинейного конденсатора можно аппроксимировать степенным полиномом, причем приемлемая точность аппроксимации в большинстве случаев получается при полиномах второй степени. Поэтому запишем аппроксимирующий полином в виде: 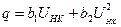, т.к. C(U)=q(U)/U, то, сделав соответствующие подстановки, найдем

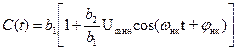(14)

Коэффициент b₁ равен дифференциальной емкости C₀ в начальной рабочей точке, заданной напряжением смещения U₀. Множитель перед косинусом имеет смысл коэффициента, характеризующего глубину изменения емкости: обозначим его m_С=(b₂/b₁)U_mНК=DC/C₀. С учетом этих обозначений соотношение (14) представляет собой зависимость емкости конденсатора изменяющейся во времени по гармоническому закону с частотой накачки:

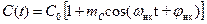(15)

Это и есть модель параметрического конденсатора, полученная из модели нелинейного конденсатора путем замены зависимости C(U) зависимостью C(t).

Рассмотрим процесс в цепи, образованной источником сигнала U_C(t)=U_mCcos(w_ct+j_c) и параметрическим конденсатором емкостью (15). Будем считать, что амплитуда сигнала мала: U_mC<<U_mНК. Поэтому для напряжения сигнала емкость С можно считать линейной, т.е. в вольт-кулонной характеристике можно ограничиться только первым слагаемым.

Найдем ток, протекающий через конденсатор:

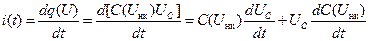(15)

Подставив в это выражение соответствующие величины, после преобразования получим:

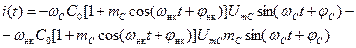
Преобразуя произведения sinacosb по известным тригонометрическим формулам, получаем:

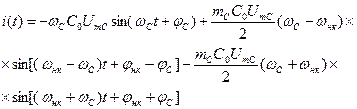(16)

Как видно из (16) в спектре тока, протекающего через параметрический конденсатор, помимо составляющей на частоте сигнала w_c содержатся гармоники разностной (w_нк-j_с) и суммарной (w_нк+j_с) частот. Рассмотрим процесс преобразования энергии в этой цепи.

Средняя мощность в рассматриваемой цепи равна мгновенной мощности, усредненной за период сигнала:

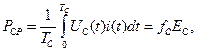(17)

где 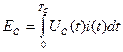- энергия сигнала, .

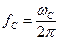Прямое интегрирование (17) с учетом (16) достаточно громоздко. Поэтому выделим вначале такую составляющую тока (16), которая дает среднею мощность отличную от нуля, а затем вычислим и среднюю мощность.

Гармоника тока на частоте сигнала является обычной реактивной составляющей тока, протекающего через конденсатор. Она находится в квадратуре с напряжением сигнала 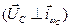и не создает средней мощности. Гармоника тока суммарной частоты тоже не дает Р_ср¹0 на частоте w_c, т.к. нет самого колебания. И только на гармоника разностной частоты, и при одном только условии w_нк=2w_с, может создать полную мощность на частоте сигнала. Обозначим ее P_{с ср} и на основании (16) и (17) найдем

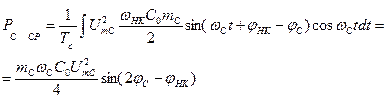(18)

Как следует из (18) средняя мощность в цепи может быть как положительной, так и отрицательной в зависимости от соотношения фазовых углов напряжений сигнала и накачки. При положительной мощности цепь потребляет от источника сигнала мощность, которая рассеивается в конденсаторе. Отрицательную мощность трактуют как мощность, поступающую в цепь от источника накачки, которая может на только скомпенсировать потери на частотах сигнала, но и привести к росту мощности сигнала на выходе цепи.

Таким образом, параметрический конденсатор может выполнять функцию активного элемента - усилителя мощности. Из (18) также следует, что по аналогии с обычным резистором, потребляющим активную мощность, параметрический конденсатор может быть заменен отрицательным сопротивлением, вносимым в цепь. Его значение можно найти из условия 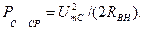Сравнивая последнее соотношение с (18), находим, что 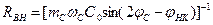и зависит только от фазовых соотношений между напряжениями сигнала и накачки.

Полученный эффект связанный с перекачкой энергии от источника U_нк в сигнал достаточно неожидан, и поэтому рассмотрим физику явления.

6.4. Параметрический резонанс.

Существуют явления, при которых, также как и при действии гармонического сигнала на колебательный контур, результат внешнего воздействия называется зависимым от частоты этого воздействия. Эти явления объединяют понятием “резонанс” в более широком смысле, и применительно к колебательным цепям, содержащих параметрический конденсатор, говорят о параметрическом резонансе.

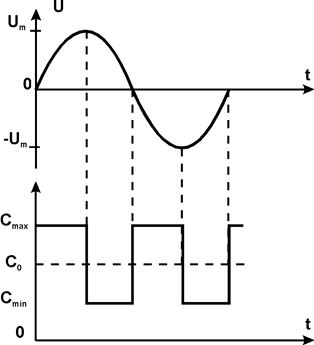
Рассмотрим в качестве примера явления, происходящие в колебательном контуре с параметрическим конденсатором при воздействии на конденсатор напряжения накачки в виде прямоугольных импульсов с частотой следования, равной удвоенной частоте собственных колебаний контура. Допустим, что между частотой собственных колебаний и изменением емкости С существует жесткая синхронизация: в моменты времени, когда напряжение на конденсаторе достигает экстремума, емкость скачком уменьшается: в моменты времени, когда напряжение становится равным нулю, емкость скачком увеличивается на ту же величину (см. рис.).

Энергия, запасенная конденсатором, равна 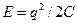. При малом приращении емкости DС<<C₀ приращение энергии

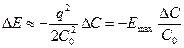(19)

(линейно зависит от приращения емкости)

Максимальная энергия, запасенная параметрическим конденсатором, равна

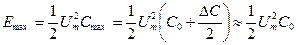
Из графиков и формулы (19) следует, что за период собственных колебаний контур дважды получает дополнительную энергию от источника накачки в моменты экстремальных значений напряжения на конденсаторе. Обозначим эту дополнительную энергию накачки Е_НК, и, в соответствии с формулой (19), запишем

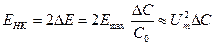(20)

Как известно, эквивалентное сопротивление контура при резонансе активно и для параллельного контура равно R_ЭКВ=rQ, где Q - добротность, а 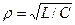- характеристическое сопротивление контура. Энергия, рассматриваемая в контуре за период собственных колебаний, равна

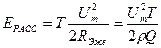(21)

Сравнивая рассеиваемую энергию (21) с накачиваемой в контур (20), можно заключить, что в контуре колебания либо не возникают, либо они нарастают неограниченно. первое происходит, если Е_РАСС>E_НК; второе - если Е_РАСС<E_НК. Другими словами, колебания нарастают, если коэффициент модуляции емкости больше некоторого критического значения. Из (20) и (21) также следует, что для возникновения параметрического резонанса необходимо, чтобы выполнить условие

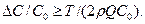
Подставив сюда 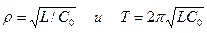, получим

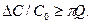
Оно и определяет критическое значение ΔС.

Поясним полученный результат. Каждый раз, когда емкость уменьшается, конденсатор заряжен и энергия источника накачки затрачивается на увеличение электрической энергии контура. Каждый раз, когда емкость увеличивается, конденсатор разряжен и изменение емкости происходит без затрат полезной энергии.

Таким образом в цепях с реактивными параметрическими элементами энергия накачки может преобразовываться в энергию сигнала.

6.5. Баланс мощностей в параметрических цепях.

Рассматриваемая модель параметрической цепи реально представляет собой нелинейную цепь. А в цепи, содержащей нелинейный конденсатор, под воздействием напряжения генератора накачки и напряжения генератора сигнала, возникают колебания комбинационных частот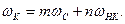

Чтобы представить себе как перераспределяется энергия информационного сигнала и сигнала накачки между комбинационным колебанием рассмотрим следующую цепь.

Пусть параллельно нелинейному конденсатору включены три цепи: цепь накачки, цепь сигнала и колебательный контур. Последний называют холостым контуром. Контур настроен на одну из комбинационных частот w_к, и, поэтому, можно принять, что других комбинационных колебаний не существует. Сумма средних мощностей колебаний сигнала P_C, накачки P_НК и комбинационной частоты P_К должна быть равна нулю(закон сохранения энергии):

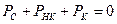(21)

Переходя в (21) от средних мощностей к энергиям в соответствии с (17) получим: 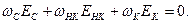Подставляя сюда 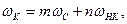находим, что

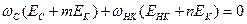(22)

Равенство (22) при произвольных 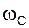и 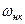выполняется, если каждое слагаемое равно нулю (поскольку они не связаны общей частотой):

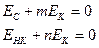
Переходя от энергии к средним мощностям получаем:

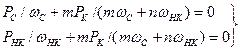(23)

Уравнения (23) выражают закон сохранения энергии в параметрических цепях. Их называют уравнениями Мэнли-Роу. И они являются частным случаем общей теоремы Мэнли-Роу о балансе мощностей в спектре колебания параметрической цепи, содержащей реактивную нелинейность (емкость или индуктивность). Теорема записывается в виде:

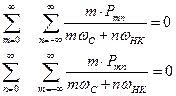
Они определяют законы распределения энергии сигнала накачки между гармониками выходного сигнала

Здесь P_mn - средняя мощность колебания на комбинационной частоте .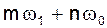

Запишем уравнения Мэнли-Роу для частного вида цепи, в которой существуют колебания только на четырех частотах:

.

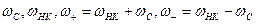Для этого в (23) необходимо задать две пары значений m и n: m=1, n=1 и m=-1, n=1.

Тогда

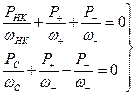(24)

Эти формулы и устанавливают количественные соотношения (баланс) между мощностями колебаний различных частот.

6.6. Параметрические усилители

На основании принципа параметрического резонанса строятся параметрические усилители. Различают три наиболее важных режима усиления: 1) с преобразованием частоты “вверх”; 2) с преобразованием частоты “вниз”; 3) регенеративный вырожденный режим.

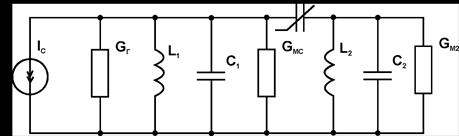
Первые два режима реализованы в двухканальном усилителе, схема которого приведена на рис. Усилитель содержит два контура: сигнальный (L₁C₁), настроенный на частоту w_с, и выходной (L₂C₂), настроенный на одну из комбинационных частот (w₊ или w_-). Режим с преобразованием частоты “вверх” или “вниз” определяется частотой настройки выходного контура. На рис. также обозначены: G_НС - проводимость нагрузки сигнального контура, G_Н2 - проводимость нагрузки холостого контура.

6.6.1. В усилителе с преобразованием частоты “вверх” выходной контур настраивается на суммарную частоту 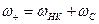и соотношение (24) принимает вид:

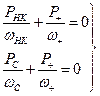(25)

Так как всегда Р₊>0 (Р₊ - мощность выделяемая в нагрузке), то из (25) следует Р_НК<0 и Р_С<0. Это означает, что оба генератора (и сигнала, и накачки) отдают мощность в выходной контур. Из второго уравнения (25) вытекает, что максимально возможный коэффициент усиления в рассматриваемом режиме равен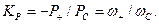

Усилители такого типа имеют ограниченное применение, поскольку на высоких частотах (там где и используется параметрические усилители) трудно обеспечить большое значение отношения 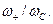Достоинством такого режима усиления является высокая устойчивость работы усиления.

6.6.2. В усилителе с преобразованием частоты “вниз” выходной контур подстраивается на резонансную частоту 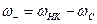и уравнение (24) принимает вид:

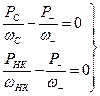(26)

Как видно из первого равенства (26), мощности Р_С и Р_- положительные, поскольку мощность, потребляемая нагрузкой - Р>0. Это означает, что часть мощности генератора накачки поступает в сигнальный контур и компенсирует часть теряемой в ней мощности, т.е. в усилителе происходит регенерация на частоте сигнала. Из (26) нельзя получить коэффициент усиления, поскольку Р_С включает не только мощность, потребляемую нагрузкой, но и часть мощности, возникающей за счет регенерации. Тем не менее, записав первое уравнение (26) в виде 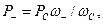можно утверждать, что усиление будет тем больше, чем больше отношение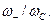

Усилители данного типа неустойчивы в работе, так как в сигнальный контур поступает мощность даже в отсутствие сигнала, что при определенных условиях может привести к самовозбуждению.

6.6.3. Одиночный регенеративный усилитель является частным случаем усилителя с преобразованием частоты “вниз”.

В этом усилителе частота накачки равна удвоенной частоте сигнала , a разностная частота - частоте сигнала 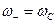поэтому отпадает необходимость в отдельном контуре, настроенном на разностную частоту. Двухконтурная схема “вырождается” в одноконтурную, откуда происходит название “вырожденный” режим. Если условие выполняется строго, в контуре выделяется одно усиленное колебание, по амплитуде равное сумме колебаний на частоте сигнала и разностной частоте. Такой режим работы называется синхронным. Как было показано, он зависит от фазовых соотношений колебаний накачки и сигнала.

В реальных условиях невозможно точно выполнить условие синхронизации. Поэтому одноконтурный регенеративный усилитель всегда работает в асинхронном режиме, когда 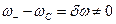. При этом величина 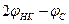становится функцией времени, поскольку получает случайную добавку dwt. Вносимое сопротивление, определяемое формулой (18), также становится случайной функцией времени и, как следствие, возникают случайные изменения усиления. Это является серьезным недостатком одноконтурных усилителей.

Параметрические усилители применяются в диапазоне частот от сотен МГц до десятков ГГц. Они имеют относительно узкую полосу пропускания 1...3% и за счет этого, а также из-за отсутствия дробового эффекта, присущего активным элементом, низкий уровень шумов.

Л. 28-30

7. Фильтрация сигналов на фоне помех.

7.1. Задачи и методы фильтрации

Электрическим фильтром называется пассивный четырехполюсник пропускающий электрические сигналы некоторой полосы частот без существенного ослабления или с усилением, а колебания вне этой полосы частот - с большим ослаблением. Такие устройства применяются для выделения полезных сигналов на фоне помех. Задача фильтрации формулируется следующим образом.

Если на вход линейного фильтра поступает смесь сигнала и помехи

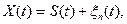(1)

то проблема состоит в том, как наилучшим образом выделить сигнал их этой смеси, т.е. как создать оптимальный фильтр. Известными считаются статические характеристики (т.е. спектр или корреляционная функция)

функции х(t), представляющей собой смесь сигнала и помехи. Искомой является периодическая функция оптимального фильтра.

Задача об оптимальной фильтрации решается по-разному в зависимости от того смысла, который вкладывается в понятие оптимальности. Рассмотрим три наиболее важных случаи оптимальной фильтрации.

1. Форма сигнала известна. От фильтра требуется только сохранение полученного сообщения, заключенного в сигнале, т.е. сохранение неискаженным помехой информационного параметра сигнала и не требуется сохранение формы. Такая задача может быть поставлена при фильтрации сигналов, форма которых известна на приемной стороне (например, обнаружение сигнала в радиотелеграфии и радиолокации). Фильтр при этом называют оптимальным, если в некоторый момент времени t₀ на его выходе обеспечивается максимальное отношение сигнала к среднеквадратическому значению напряжения шума. Такой фильтр может быть интегратором, поскольку речь идет о типовом значении полезного сигнла. При этом он должен лучше пропускать те частоты, на которых больше интенсивность спектральных составляющих сигнала и меньше интенсивность помех.

Для передаточной функции только оптимального фильтра теория дает следующие выражения:

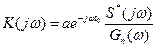(2)

где а - некоторая постоянная;

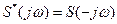- величина, комплексно сопряженная амплитудному спектру сигнала;

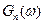- спектр мощности помехи.

В случае помехи с равномерным спектром частная характеристика оптимального фильтра с точностью до постоянного множителя совпадает с амплитудным спектром сигнал:

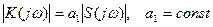(3)

Отсюда специфическое название подобных оптимальных фильтров - согласованные фильтры (т.е. согласованные с сигналом).

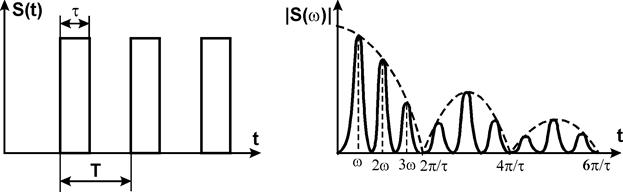
Например, при приеме сигнала в виде передаточной повторяющихся импульсов, спектр каждого из которых состоит из отдельных узких полос (см. рис.), фильтр должен пропускать лишь эти полосы.

Рассматриваемый сигнал пройдет через такой фильтр без искажений, а мощность помехи уменьшится, т.к. она будет складываться из мощностей лишь тех спектральных составляющих помехи, которые попадут в полосу прозрачности фильтра. Такой фильтр для приема последовательностей импульсов получил название гребенчатого фильтра. Его применение приводит к тем большему увеличению превышения сигнала над помехой, чем уже полоса прозрачности фильтра. В свою очередь полосы прозрачности могут быть сделаны тем более узкими, чем больше характер последовательности приближается к периодическому закону (в этом случае полосы спектра превращается в линии). Но приближение к периодическому сигналу, т.е. достаточно многократное его повторение, эквивалентное увеличению длительности сигнала. Таким образом, согласованная фильтрация повышает помехоустойчивость как бы за счет увеличения длительности полезного сигнала.

2. Форма сигнала неизвестна, а от фильтра требуется ее сохранения. Например, фильтрация после детектора должна обеспечивать наилучшее воспроизведение на фоне шума не одного или нескольких параметров сигнала, а всего сигнала S(t). В этом случае в качестве критерия оптимальности (точности воспроизведения сигнала) удобно принять среднеквадратичнную ошибку, т.е. средний квадрат уклонения воспроизведенного сигнала от периодического. если сигнал и помеха являются независимыми и стационарными случайными процессами, то частотная характеристика такого оптимального фильтра, обеспечивающего минимальную среднеквадратичную ошибку, определяется спектрами мощности сигналом Р_С(w) и помехи G_П(w).

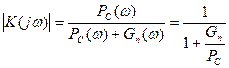(4)

Фильтр ослабляет те спектральные составляющие, которые сильней поражены помехой, и для которых больше отношение G_П(w)/ Р_С(w). А на тех частотах, где помеха отсутствует G_П(w)<< Р_С(w), коэффициент передачи K→1.

3. Выделение длительного периодического сигнала из его смеси с помехой может быть осуществлено путем исследования функции корреляции этой смеси. Корреляционный фильтр, осуществляющий такое исследование, содержит блок переключения и блок усреднения (интегратор).

При взаимокорреляционной фильтрации, когда фильтр, располагая образцом сигнала, определяет функцию взаимной корреляции между принятой смесью X(t) и образцом сигнала S(t) (в данном случае речь идет только о констатации факта наличия сигнала):

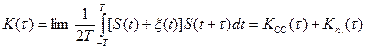
Если сигнал и помеха некоррелированы, то 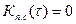и напряжения 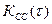будет свидетельствовать о наличие сигнала в смеси.

Автокорреляционная фильтра используется при отсутствии определенных сведений о форме сигнала. Фильтр в этом случае определяет автокорреляционную функцию смеси:

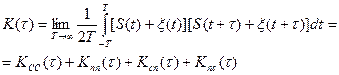
При отсутствии корреляции между сигналом и помехой последние два слагаемых исчезнут. Что касается оставшихся двух слагаемых, то первое из них может носить черты периодичности, т.к. является автокорреляционной функцией сигнала близкого к периодическому, а второе обращается в ноль, если сдвиг t больше интервала корреляции помехи t_П. Таким образом, при достаточно большом сдвиге t и времени усреднения Т наличие напряжения K_C.C(t) на выходе коррелятора свидетельствует о наличии периодического сигнала в смеси.

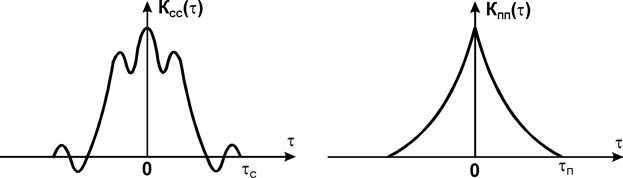
Однако реальные сигналы связи не являются периодическими и ограничены некоторой длительностью t_с. Следовательно, при t> t_с автокорреляционная функция сигнала становится равной нулю (см. рис.). С другой стороны, интервал корреляции помехи t_П возрастает тем больше, чем большему ограничению подвергается спектр помехи в фильтре, поскольку помеха приобретает характер периодичности. При оптимальной фильтрации до коррелометра t_П может превысить t_с и корреляционная фильтрация не даст никакого эффекта.

Таким образом, автокорреляционная фильтрация эффективна только в том случае, если t_с> t_П, т.е. при широкой полосе пропускания фильтровых цепей и достаточно длительных сигналов. Повышение помехоустойчивости сигнала по длительности над помехой.

7.2. Согласованная фильтрация заданного сигнала