Появление быстродействующих многоразрядных процессоров цифровой обработки сигналов самых различных типов сделало возможным производить цифровую обработку сигналов не только речи и вещания, но и телевидения. Однако, даже при такой совершенной технике необходимо учитывать погрешности работы ЦФ, обусловленную квантованием уровней сигналов.
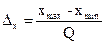 |
Пусть хmax и xmin – наибольшее и наименьшее значение уровня сигнала на выходе аналого-цифрового преобразователя (АЦП). Если для квантования сигналов используется Q уровней, то при равномерном квантовании шаг квантования определяется соотношением
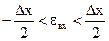 |
Квантованные отсчеты хкв(k) описывают мгновенные значения аналогового дискретного сигнала x(k) с определенной погрешностью (с шумом квантования): ε(k)=xкв(k)-x(k). Эта погрешность уменьшается (по модулю) с уменьшением Δх. Будем считать, что квантователь работает по следующим правилам: в качестве дискретного принимается уровень, ближайший к истинному. Если действительный входной уровень x(k) находится в середине между дискретными номерами q и (q+1) – выбирается любой из них. При оговоренных условиях погрешность εвх(k) лежит в пределах
Чаще всего считается, что случайная погрешность Eвх (при
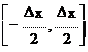 |
различных k) равномерно распределена на отрезке. Тогда
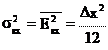 ее математическое ожидание (МО) равно нулю, а дисперсия
ее математическое ожидание (МО) равно нулю, а дисперсия
Определим погрешность работы линейного
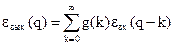 |
стационарного фильтра, обусловленную шумом квантования εвх(k). Дискретный входной отсчет ЦФ, обусловленный шумом квантования εвх(k), согласно (41) равен
Математическое ожидание выходного шума Eвых=0. Для нахождения дисперсии выходного шума 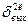 предположим, что отдельные отсчеты входного шума Eвх(k) – независимые случайные величины с
предположим, что отдельные отсчеты входного шума Eвх(k) – независимые случайные величины с
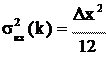 |
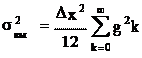 равномерным распределением и дисперсией. Тогда
равномерным распределением и дисперсией. Тогда
.
Выходной шум ЦФ, обусловленный квантованием сигнала, тем меньше, чем быстрее убывают отсчеты импульсной характеристики фильтра. Относительную погрешность ЦФ, обусловленную шумом квантования, можно определить так
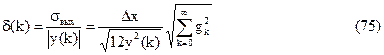 |
Оценим влияние шума квантования на работу цифрового перемножителя. Из-за шума квантования квантованные отсчеты входного и опорного сигналов можно записать в виде
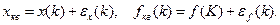
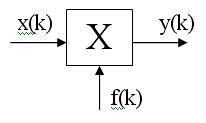 Тогда
Тогда
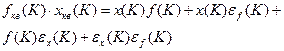
Схема цифрового
перемножителя
Ошибка цифрового перемножителя из-за шума квантования будет такой
Eвых(k)=x(k)Ef(k)+f(k)Ex(x)+Ex(k)Ef(k)
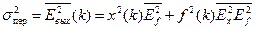 |
При сделанных ранее предположениях о шуме квантования математическое ожидание
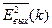 . Предполагая шумы квантования сигналов x(t) и f(t) независимыми стационарными случайными процессами, получаем для дисперсии выходного шума перемножителя следующее выражение
. Предполагая шумы квантования сигналов x(t) и f(t) независимыми стационарными случайными процессами, получаем для дисперсии выходного шума перемножителя следующее выражение
Если сигналы x(t) и f(t) квантуются с одинаковым шагом D x=Dt=p, то
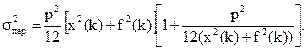 |
Относительная погрешность работы цифрового перемножителя, обусловленная шумом квантования, будет такой
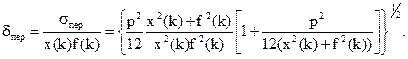 |
 2015-05-06
2015-05-06 375
375








