В общем случае в линейном стационарном цифровом фильтре k-й выходной отсчет y(k) (в момент времени t=kΔ) линейно зависит от k-го входного отсчета x(k) и некоторого количества предшествующих отсчетов x(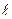 ) (
) (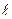 <k), а также от некоторого количества выходных отсчетов y(
<k), а также от некоторого количества выходных отсчетов y(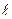 ) (
) (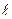 <k):
<k):
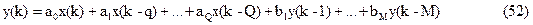 |
Числа L и M в разностном уравнении (52) называют соответственно относительной памятью ЦФ по входу и выходу. ЦФ с памятью по входу называются рекурсивным, а без такой памяти нерекурсивными.
Алгоритмы работы различных ЦФ отличаются параметрами Q и M и набором коэффициентов {aℓ} и {bi}. Рассмотрим сначала реализацию нерекурсивных ЦФ, когда все bi=0 (т.е. М=0).
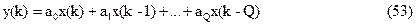 |
В этом случае разностное уравнение (52) принимает вид:
Структурная схема ЦФ, реализующая алгоритм (53) приведена на следующем рисунке:

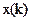 |
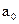 | 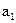 | 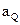 | |||
 |  |  | |||||||
 | |||||||||
 | |||||||||

 | |||
 | |||
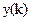 |
 2015-05-06
2015-05-06 247
247








