Спектры непериодических сигналов. Непериодический сигнал может быть представлен в виде гармонических составляющих, частоты которых, однако

Непериодический сигнал 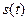может быть представлен в виде гармонических составляющих, частоты которых, однако, не являются дискретными, а пробегают непрерывную совокупность значений. Эта задача решается с помощью интегральных преобразований Фурье. Спектр сигнала может быть найден из соотношения

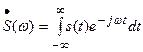. (6.16)

Здесь называется спектральной плотностью сигнала, или спектральной характеристикой функции .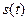

Обратное преобразование Фурье позволяет перейти от спектральной плотности к форме сигнала:

. (6.17)

Таким образом, с помощью преобразований Фурье сигналы любой формы могут быть представлены в виде совокупности гармонических составляющих с известными амплитудами и фазами, а сам гармонический сигнал становится как бы элементарным пробным сигналом при анализе цепей. Причем математические преобразования существенно упрощают, если гармонический сигнал, например напряжение

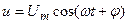
Представить в комплексной форме:

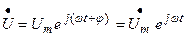(6.18)

Если на каком-то участке линейной цепи действует гармоническая ЭДС, то на любом другом участке этой цепи может появиться только гармонический сигнал.

Комплексный коэффициент передачи

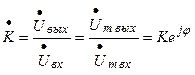, (6.19)

где .

Если на выходе цепи с известным коэффициентом передачи действует произвольный сигнал 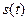, то сигнал на выходе цепи можно определить следующим образом: по (6.16) найти спектральную плотность , вычислить спектр сигнала на выходе цепи как

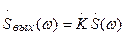. (6.20)

И наконец, по (1.17) установить форму выходного сигнала

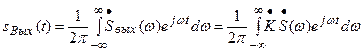(6.21)

Коэффициент передачи 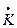остается под интегралом, так как зависит от частоты.

К сожалению, преобразование Фурье применимо только тогда, когда функция 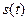– абсолютно интегрируема. Для этого необходимо, чтобы интеграл 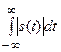сходился, т. е. был равен конечной величине. При невыполнении этого условия следует использовать иные способы преобразования.

Определим спектры некоторых наиболее распространенных сигналов.

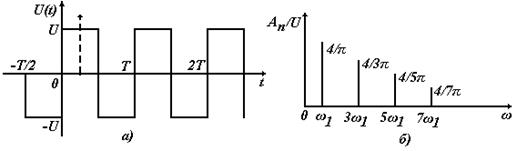
Рис. 6.2. Сигнал вида меандр (а) и его амплитудный спектр (б)

1. Периодическая последовательность колебаний прямоугольной формы (меандр) с амплитудой U (см. рис. 6.2 а)

Согласно первому уравнению(6.8)

; .

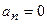В соответствии со вторым уравнением (6.8)

.

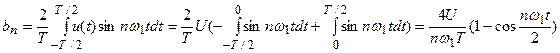Учитывая, что 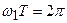, получаем

Подставляя эти значения коэффициентов в (6.7), запишем ряд Фурье

. (6.22)

Если отсчет времени начинать с середины импульса (на рис. 6.2 а показано пунктиром), то 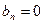и ряд Фурье принимает вид

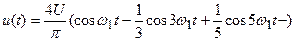. (6.23)

Из (6.22) и (5.23) видно, что меандр имеет линейчатый спектр (рис. 6.2 б).

Заметим, что из-за наличия точек разрыва ряд Фурье с вычисленными коэффициентами не сходится при 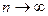в этих точках к 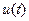. Тем не менее при 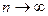сумма ряда приближается к 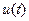во всех остальных точках.

2. Одиночный импульс прямоугольной формы. В соответствии с (6.16) спектральная плотность импульса длительности 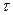и амплитуды U имеет вид (рис. 6.3 б)

. (6.24)

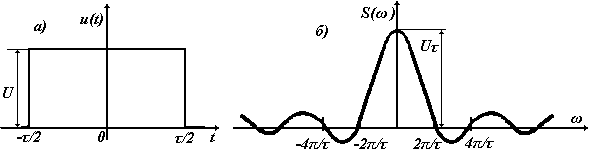
Рис. 6.3. Прямоугольный импульс (а) и его спектральная плотность (б)

Воспользовавшись уравнениями Эйлера, получаем

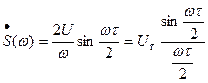(6.25)

6.4. Представление отклика линейной цепи в форме интеграла наложения или свертки

Любой детерминированный сигнал можно представить при помощи единичной ступенчатой или единичной импульса функции, называемых в радиоэлектронике единичная ступенька и единичный импульс.

Единичная ступенька (скачок):

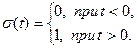(6.26)

Она равна нулю при отрицательных значениях аргумента и единице при положительных. Сдвиг ступеньки по оси времени на интервал 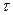видоизменяет выражение (6.26) в

(6.27)

Произвольная ограниченная функция времени 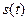, умноженная на 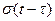, обращается в нуль («отсекается») при 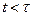и остается без изменений при 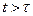. Таким образом, умножение 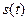на 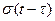равносильно замыканию ключа, включающего сигнал в момент времени .

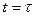Единичный импульс (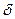 -функция, функция Дирака):

(6.28)

При одновременном выполнении условия

(6.29)

При сдвиге импульса по оси времени на интервал 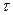выражения (6.28) и (6.29) принимают вид

(6.30)

Единичный импульс представляет собой производную от единичной ступеньки:

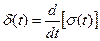, (6.31)

а единичная ступенька – интеграл от единичного импульса:

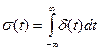(6.32)

Если умножить подынтегральное выражение (6.30)на функцию 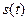, то не равное нулю значение произведения может иметь место только при 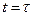, поэтому

(6.33)

Таким образом, единичный импульс 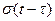производит выборку отдельных значений 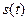или стробирует функцию 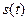в момент времени .

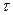Отклик (реакция) системы на единичную ступеньку называется переходной характеристикой 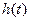, отклик системы на единичный импульс – импульсная характеристика - 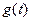. Импульсная характеристика определяется как производная от переходной: 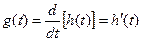, (6.34)

а переходная – интегралом от импульса:

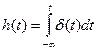(6.35)

Пусть к системе с импульсной характеристикой 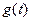приложен сигнал 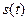. С некоторым приближением этот сигнал можно рассматривать как последовательность плотно прилегающих друг к другу коротких импульсов длительностью 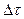с амплитудами, равными мгновенным значениям сигнала 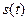в момент времени 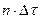где n - порядковый номер импульса (рис1.4). Заменим короткие импульсы единичными в моменты времени 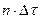, а их амплитуды приравняем к площадям прямоугольников 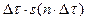. При стремлении 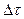к нулю точность такого представления функции 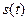возрастает.

Рис. 1.4. Сигнал в виде последовательности импульсов

Отклик на n -й импульс пропорционален импульсной характеристике системы, смещенной на время :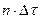

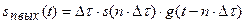(6.36)

В соответствии с принципом суперпозиции отклик на сигнал в целом есть сумма откликов на все элементарные импульсы:

. (6.37)

Или в пределе 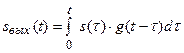(6.38)

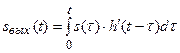(6.39)

Выражение (6.38) и (6.39) называют интегралом свертки (интегралом Дюамеля).

Единичные ступеньки и импульс являются идеализацией, на практике мгновенными считают явления, продолжительность которых существенно меньше длительности переходных процессов в исследуемой цепи.