Если в спектре сигнала нет составляющих с частотой выше 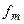 , то такая частота называется предельной частотой в спектре сигнала
, то такая частота называется предельной частотой в спектре сигнала 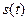 и её спектральная плотность на частотах выше
и её спектральная плотность на частотах выше 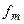 равна нулю (
равна нулю (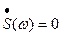 , при
, при 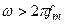 ).
).
Один из вариантов представления сигналов в виде (6.3) – разложение их по функциям 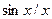 (sinc (x), см. рис.6.5), получившее широкое распространение в связи с научными работами Котельникова В.А. (1933 год).
(sinc (x), см. рис.6.5), получившее широкое распространение в связи с научными работами Котельникова В.А. (1933 год).
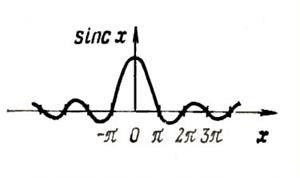
Рис. 6.5. График функции sinc x=(sin x)/x
Соответствующая теорема (В.А. Котельникова) гласит: если наивысшая частота в спектре функции 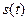 меньше
меньше 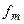 , то функция
, то функция 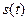 полностью определяется последовательностью своих мгновенных значений через интервалы времени, не превышающие
полностью определяется последовательностью своих мгновенных значений через интервалы времени, не превышающие 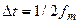 .
.
Сигнал 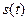 может быть точно восстановлен согласно выражению, называемому рядом Котельникова:
может быть точно восстановлен согласно выражению, называемому рядом Котельникова:
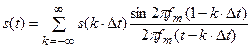 (6.40)
(6.40)
Первые множители слагаемых в (6.40) 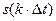 представляют собой отсчеты сигналов в момент времени
представляют собой отсчеты сигналов в момент времени 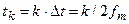 , вторые - функцию вида
, вторые - функцию вида 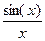 . В действительности отсчеты мгновенных значений сигналов могут быть сделаны лишь в интервале наблюдения
. В действительности отсчеты мгновенных значений сигналов могут быть сделаны лишь в интервале наблюдения 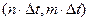 , где n и m – целые числа. В соответствии с этим сигнал восстанавливается не по (6.40), а с некоторой погрешностью рядов вида:
, где n и m – целые числа. В соответствии с этим сигнал восстанавливается не по (6.40), а с некоторой погрешностью рядов вида:
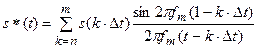 (6.41)
(6.41)
Все реальные радиоэлектронные устройства имеют ограниченную полосу пропускания, и определение частоты 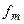 не представляет особых трудностей. Основываясь на теореме Котельникова, в большом числе практически важных случаев можно регистрировать только мгновенные значения сигнала и впоследствии восстановить этот сигнал полностью с заранее известной погрешностью.
не представляет особых трудностей. Основываясь на теореме Котельникова, в большом числе практически важных случаев можно регистрировать только мгновенные значения сигнала и впоследствии восстановить этот сигнал полностью с заранее известной погрешностью.
Представление непрерывного сигнала рядом вида (6.41) – один из способов дискретизации сигнала. В некотором смысле Фурье-разложение периодического сигнала, например представление его в виде (6.9), также является дискретизацией, так как непрерывная совокупность значений 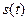 заменяется при этом дискретным набором амплитуд
заменяется при этом дискретным набором амплитуд 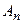 и фаз
и фаз 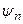 гармоник. Принципиальное отличие дискретизации с использованием ряда (6.40) заключается в том, что отсчеты мгновенных значений сигнала производятся непосредственно в процессе его поступления на вход преобразующего устройства, а для представления в виде (6.9) необходимо предварительно полностью зарегистрировать сигнал. Иными словами, для вычитания
гармоник. Принципиальное отличие дискретизации с использованием ряда (6.40) заключается в том, что отсчеты мгновенных значений сигнала производятся непосредственно в процессе его поступления на вход преобразующего устройства, а для представления в виде (6.9) необходимо предварительно полностью зарегистрировать сигнал. Иными словами, для вычитания 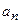 и
и 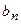 или
или 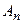 нужно знать
нужно знать 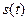 (см.(8.8), (6.10), (6.16)), а для определения
(см.(8.8), (6.10), (6.16)), а для определения 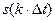 этого не требуется.
этого не требуется.
Полученные в результате дискретизации мгновенные значения сигнала могут быть любыми в диапазоне от 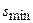 до
до 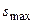 и относиться, таким образом, к непрерывному множеству значений. Переход от этого непрерывного множества к конечному набору дискретных значений называют квантованием. При квантовании в диапазоне
и относиться, таким образом, к непрерывному множеству значений. Переход от этого непрерывного множества к конечному набору дискретных значений называют квантованием. При квантовании в диапазоне 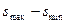 фиксируется ряд дискретных уровней
фиксируется ряд дискретных уровней 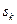 . Наиболее широко распространены устройства квантования с одинаковыми расстояниями между соседними уровнями
. Наиболее широко распространены устройства квантования с одинаковыми расстояниями между соседними уровнями 
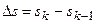 .
.
 2015-05-06
2015-05-06 1856
1856








