2015-05-06
440
Периодический сигнал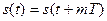 
с частотой повторения 
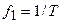и угловой частотой 
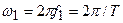может быть представлен в виде ряда Фурье
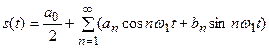, (6.7)
где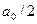 
– среднее значение за период, или постоянная составляющая сигнала; коэффициенты 
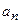и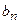 
называются соответственно амплитудами косинусоидальных и синусоидальных составляющих и вычисляются по формулам
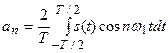, n=0,1,2,…, (6.8)
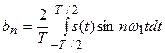, n=1,2,….
Выражение (6.7) является суммой косинусоид и синусоид с частотами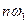 
, что эквивалентно сумме только синусоид или космнусоид, но с различными фазами, например:
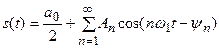, (6.9)
Модуль амплитуды 
и фаза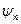 
каждой гармоники определяется для (6.9) выражениями
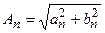; (6.10)
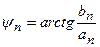. (6.11)
Совокупность значени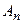й 
и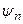 
называется спектром функции 
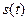, определяется (6.7). Согласно (6.9) спектр периодического сигнала является линейчатым, или дискретным, состоящим из отдельных линий (гармоник), соответствующих частотам 
, 
, 
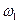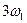… (рис. 6.1). Для полной характеристики сигнала необходимо знать фазу каждой гармоники 
.
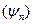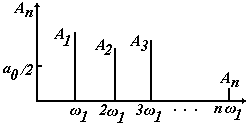
Рис. 6.1. Амплитудный спектр периодического сигнала
Вычисление коэффициентов и многие другие математические процедуры упрощаются при использовании вместо тригонометрических форм (6.7) и (6.9) комплексной записи ряда Фурье:
|
|
|
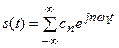. (6.12)
Коэффициенты 
, называемые комплексными амплитудами, равны:
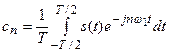(6.13)
и связаны с 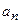, 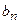и 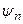выражениями
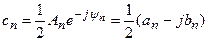при n >0,
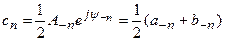при n <0. (6.14)
Переход от комплексной формы к тригонометрической производят в конце анализа, используя формулы Эйлера
; 
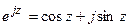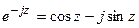; (6.15 a)
; 
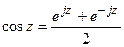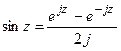. (6.15 б)
