Распределение мощности в спектре периодического колебания

Пусть колебание 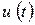(ток, напряжение) представляет собой сложную периодическую функцию времени с периодом .

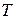Энергия такого колебания, длящегося от 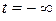до 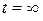, бесконечно велика. Основной интерес представляет средняя мощ­ность периодического колебания и распределение этой мощности между отдельными гармониками. Очевидно, что средняя мощность колебания, рассматриваемого на всей оси времени, совпадает с мощностью, средней за один период .

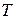Среднюю мощность периодического колебания можно вычислить

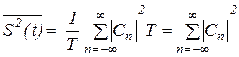. (1.11)

Используя тригонометрическую форму ряда Фурье и учитывая, что 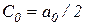и 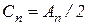, получаем

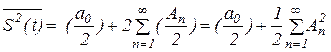. (1.12)

Если 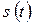представляет собой ток 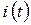, то при прохождении его через сопротивление 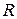выделяется мощность (средняя)

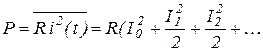, (1.13)

где 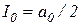− постоянная составляющая, а 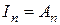− амплитуда 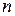− гармоники тока .

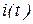Итак, полная мощность равна сумме средних мощностей, выде­ляемых отдельно постоянной составляющей 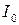и гармониками с амплитудами 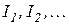Это означает, что средняя мощность не за­висит от фаз отдельных гармоник.