Скорость звука, максимальная скорость, критическая скорость

Безразмерные скорости. Число Маха.

Приведенная и относительная скорости. Коэффициенты скорости.

Распространение слабых возмущений в потоке газа.

В газовой динамике широко применяются характерные скорости: скорость распространения звука, максимальная скорость течения газа и критическая скорость. Рассмотрим эти понятия подробнее.

Скорость звука – скорость распространения в упругой среде малых возмущений. Малыми или слабыми принято называть такие возмущения среды, в которых местное изменение давления среды в точке возмущения, т.е. амплитуда давления, пренебрежимо мало по сравнению с общим давлением.

Звук, распространяется в виде слабых волн давления в упругой среде. Эти волны являются продольными. От источника слабых возмущений или источника звука они распространяются в неподвижной среде в виде сферических поверхностей. Скорость, с которой перемещается такая волна, называется скоростью распространения звука, или просто скоростью звука. Понятие скорости звука является одним из важнейших в теории течения сжимаемой жидкости.

Рассмотрим процесс распространения малого (слабого) возмущения в сжимаемой среде. Пусть неподвижная сжимаемая жидкость с заданными параметрами r, p, T находится в длинной трубе постоянного по длине сечения, ограниченной слева поршнем (см. рисунок 13). В некоторый момент времени поршень начинает двигаться слева направо с постоянной скоростью w и «наталкивается» на неподвижную жидкость. «Слой» жидкости, непосредственно примыкающий к поршню, в результате движения поршня несколько уплотняется (сжимается) и давление в нем повышается – до величины p+dp; кроме того, жидкость в этом «слое» из состояния покоя приходит в движение со скоростью w. Далее сжимается и приходит в движение «слой» жидкости, примыкающий к «первому слою», и т.д. Можно представить себе движущуюся в жидкости «слабую волну сжатия», подобную той, которая возникает при страгивание с места длинного железнодорожного состава – вагоны не одновременно, а последовательно (поочерёдно) приходят в движение благодаря упругости сцепки. Другим примером может служить картина падающих костяшек домино, выстроенных в длинный ряд.

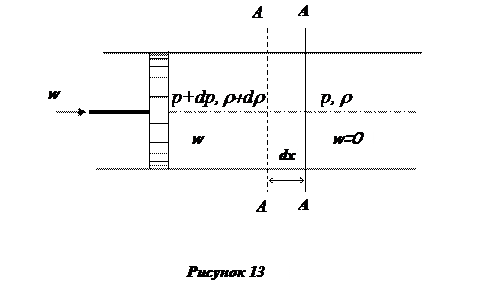
Таким образом, в жидкости распространяется слабая волна сжатия, фронт которой можно представить в виде перемещающегося вдоль трубы (точнее - вдоль жидкости) сечения А-А, отделяющего сжатую – «возмущённую», область жидкости с параметрами p+dp, r+dr, T+dT (слева от сечения А-А)от невозмущённой области жидкости, т.е. области, куда возмущения ещё не проникли (справа от сечения А-А).

Если перемещение сечения А-А за время dt обозначить dx, то скорость распространения фронта слабой волны в этом случае может быть выражена как dx/ dt. Скорость движения фронта слабой волны относительно жидкости называют скоростью звука и обозначают обычно а. «Относительность» особенно важно иметь в виду, поскольку жидкость в общем случае в момент возникновения в ней возмущения не обязательно должна находиться в состоянии покоя, а может изначально двигаться с некоторой скоростью.

За время dt фронт волны – сечение А-А, переместится на расстояние dx = a× dt и при этом будет сжат «новый слой» жидкости, т.е. произойдет уплотнение жидкости - увеличение плотности распределения массы в элементарном объёме dV = Fdx = Fadt, заключённом между начальным и конечным в указанный промежуток времени положениями сечения А-А. Поскольку в рассматриваемом элементарном объёме dV нет источников и стоков, то приращение массы жидкости в этом объёме может происходить только за счет притока в него за время dt некоторого количества жидкости из «возмущённой» области со скоростью w.

Очевидно, что из уравнения неразрывности для рассматриваемого случая:

dV× dr = (r+dr)×F×w× dt или F× a× dt× dr = (r+dr)×F×w× dt,

где F – площадь поперечного сечения трубы, dV× dr - изменение массы жидкости в элементарном объёме dV; (r+dr)×F×w× dt – масса жидкости, притекающая в элементарный объём dV за время dt; с точностью до малых величин первого порядка (пренебрегая бесконечно малой величиной второго порядка F×W× dr× dt) можно получить следующее соотношение:

a× dr = rw. (1)

Применим к рассматриваемому элементарному объёму dV закон о сохранении количества движения, не учитывая при этом действия сил трения в жидкости (допустим, что жидкость идеальная). Изменение количества движения элементарного объёма d(mw) (здесь m – масса элементарного объёма) должно быть равно импульсу внешних сил, приложенных к этому объёму. В рассматриваемом случае в качестве внешних сил выступает только поверхностная сила, обусловленная разностью (градиентом) давления в звуковой волне dp. Заменяя массу произведением плотности на объём, и учитывая, что скорость движения рассматриваемого объёма в начальный момент времени (до прохождения через него фронта волны) была равна нулю, получим уравнение движения (уравнение количества движения) для рассматриваемого элементарного объёма:

(r+dr)×F× a×w× dt = F× dp× dt,

где слева стоит приращение количества движения элемента, а справа – импульс сил, действующих на элемент за время dt. Из уравнения движения, рассуждая аналогично предыдущему (пренебрегая бесконечно малой величиной второго порядка F× a×w× dr× dt), получим ещё одно соотношение

arw = dp. (2)

Исключив из полученных соотношений (1) и (2) скорость w, получим уравнение для определения скорости звука:

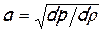. (3)

Для того чтобы воспользоваться уравнением (3) нужно знать, как происходит процесс распространения звуковых волн, т.е. для каких условий следует вычислять производную dp/dr.

Одним из первых, кто практически решил эту задачу, был Исаак Ньютон. Он вычислил скорость звука в воздухе при атмосферном давлении и комнатной температуре (при этих параметрах воздух с хорошим приближением можно рассматривать как совершенный газ, для которого справедливо уравнение состояния p=rRT). Ньютон считал, что процесс распространения звука в воздухе происходит в изотермических условиях и производную надо брать при постоянной температуре, т.е. при условии T=const. Воспользовавшись уравнением Бойля-Мариотта для изотермического процесса в совершенном газе pv= const или p=r×const, для производной получим

,

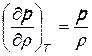а для скорости звука

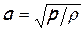. (4)

Однако при прямых измерениях скорости звука в воздухе было получено значение а примерно на 20% превосходящее величину, вычисленную Ньютоном. Причина этих расхождений была установлена Лапласом, который отметил, что поскольку звуковые колебания (волны) в упругой среде (воздухе) распространяются очень быстро, то можно предположить, что сколь-нибудь заметного теплообмена между зонами разряжения и сжатия звуковой волны и окружающей средой при этом не успевает произойти (что, кстати, хорошо подтверждается опытом). Поэтому, процесс распространения звуковой волны можно считать адиабатным и изоэнтропийным и производную в (3) нужно брать при постоянной энтропии, т.е. при условии S=const.

Уравнение Лапласа для скорости звука

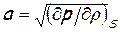. (5)

В случае изоэнтропийного процесса плотность и давление будут связаны уравнением изоэнтропы p/r^k =const. Тогда dp = k×r^k-1× dr×const и dp/dr = k ×r^k-1×const, определяя постоянную из уравнения изоэнтропы, для производной (¶p/¶r)_S получим

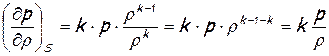, (6)

а для скорости звука

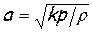. (7)

Для совершенного газа,имея в виду, что p/r = RT, может быть установлена однозначная связь скорости звука с абсолютной температурой газа

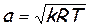. (8)

Из соотношения (8) видно что, чем выше температура газа, тем больше скорость распространения звуковых волн в нём. Кроме того, скорость звука зависит от физических свойств газа (k и R). Этот вывод находится в полном соответствии с газокинетическими представлениями о процессе распространения малых возмущений в среде, состоящей из движущихся молекул. Скорость распространения возмущений должна зависеть от скорости движения молекул, которая, в свою очередь, определяется температурой. Известно, что скорость движения молекул газа (средняя скорость) близка к скорости звука. В этой связи необходимо подчеркнуть, что квадрат числа Маха M²=w²/a² определяет соотношение в потоке средней кинетической энергии направленного движения газа как целого и средней кинетической энергии беспорядочного движения молекул, т.е. частиц, составляющих это целое.

Следует иметь в виду, что формула (7), как и уравнение Лапласа (5) справедливы и для газов и для капельных жидкостей и для твердых упругих тел, в то время как формула (8) имеет отношение только к совершенному газу. В несжимаемых средах r = const, dr= 0 и a=∞, т.е. звуковые волны распространяются мгновенно.

***

«Скорость звука выражается следующей зависимостью:

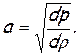(2.34)

… Чтобы рассчитать производную, входящую в выражение (2.34), воспользуемся уравнением политропного процесса

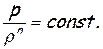
Логарифмируя и дифференцируя его, получим

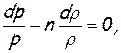
откуда

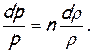(2.35)

Численное значение показателя политропы зависит от того, какой термодинамический процесс происходит при сжатии и расширении газа внутри слабых волн возмущения.

В 1687 году Ньюто н высказал предположение, что производная 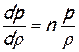. С термо­динами­ческой точки зрения это условие отвечает изотермному процессу (n=1), следовательно, оно равносильно допущению о том, что внутри волн в местах повышенного и пониженного давления («гребнях» и «впадинах») температура одинакова. Такой процесс можно представить лишь в том случае, если допустить, что волны распространяются настолько медленно, что тепло из области «гребней» успевает отводиться в область «впадин» и температура выравнивается по всему объему. Сравнение формулы Ньютона

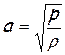
с результатами опытов по измерению скорости звука в воздухе, проведенных много позже, показало, что расчетная скорость звука получается значительно ниже действительной.

В 1810 году Лаплас предположил, что сжатие и расширение газа внутри волн происходит без подвода и отвода тепла, т.е. изоэнтропически. Тогда n=k и

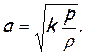(2.36)

Эта формула дает очень хорошее совпадение с экспериментом и применяется до настоящего времени. Заменив в формуле (2.36)

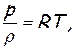
можно представить ее в таком виде:

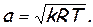(2.37)

Для воздуха 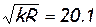, следовательно,

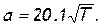(2.38)

Таким образом, скорость звука однозначно определяется температурой. При нормальной температуре Т=288К она равна а=341 м/сек.»

& (Виноградов) с.47 … 48

Рассмотрим понятие максимальной скорости течения газа. Из уравнения энергии, записанного для движущегося и заторможенного газа в энергоизолированном потоке,

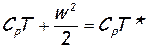
следует, что при постоянной температуре торможения, чем выше скорость потока, тем ниже истинная температура газа. Такое явление имеет место, например, при истечении газа из резервуара через сопло, в котором отсутствует теплообмен с окружающей средой. Пределом является случай, когда Т=0. Скорость тогда достигает максимально возможного значения, равного w_mах. Дальнейшее увеличение скорости невозможно, так как газ уже полностью исчерпал запас энтальпии h=C_pT, а внешнего притока энергии нет. Таким образом,

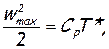
откуда

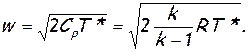(2.39)

Для воздуха

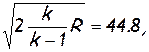
тогда

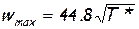м/сек. (2.40)

Так например, при Т=288°К, т.е. при нормальной температуре w_mах=762 м/сек.

Максимальную скорость можно трактовать так же, как скорость истечения в пустоту. Действительно, если из некоторого резервуара (рис.14), объем которого достаточно велик, происходит идеальное истечение газа через сопло, то скорость истечения легко определяется на основании следующих соображений. Так как объем резервуара велик, то скорость внутри него близка к нулю. Параметры состояния газа в резервуаре поэтому можно считать равными параметрам торможения р * и Т *. Решив уравнение (2.27) [1] относительно скорости

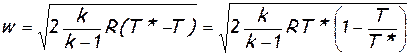
и заменив отношение температур с помощью уравнений (2.33)[2], получим формулу скорости истечения

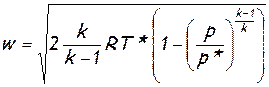. (2.41)

Из формулы (2.41)[3] видно, что при понижении давления той среды, в которую происходит истечение — р, скорость истечения возрастает. Если давление р упадет до нуля, то скорость достигает максимального значения: формула (2.41) приобретает вид (2.39).

Нужно заметить, что поскольку температура, равная абсолютному нулю, недостижима, то практически невозможно получить и максимальную скорость газа. Поэтому ее следует рассматривать как теоретический предел скорости течения газа.

Понятие критической скорости удобно ввести, рассматривая процесс истечения газа из резервуара через сопло в атмосферу, хотя эта величина применяется в самых разнообразных задачах, не обязательно связанных с процессом истечения. На рис.14 внизу изображены кривые изменения скорости потока, температуры и местной скорости звука по длине сопла, через которое движется газ. Это течение является энергоизолированным, поэтому связь между скоростью и температурой выражается с помощью уравнения энергии в форме (2.19)[4]. По мере нарастания скорости по длине сопла, температура, как это следует из уравнения энергии (2.19), а следовательно, и скорость звука (2.37) уменьшаются. Таким образом; в различных сечениях одного и того же потока скорость звука получается разной. В начале сопла скорость потока ниже скорости звука, в конце — превышает ее. Где-то в средней части сопла существует сечение, в котором скорость потока равна местной скорости звука. Это сечение называется критическим, а параметры потока в нем — критическими параметрами. Ниже будет показано, что если газ движется без трения и без обмена энергией с внешней средой, то критическое сечение совпадает с самым узким местом канала — горлом сопла.

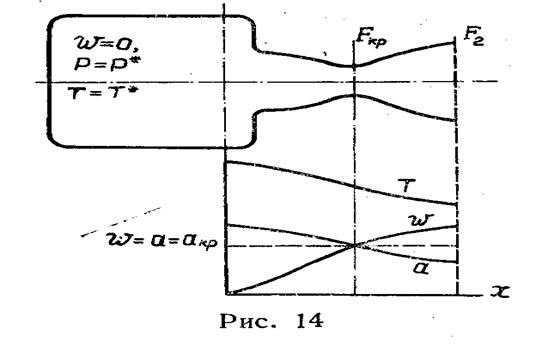
Можно так сформулировать понятие критической скорости: критической скоростью называется такая скорость течения газа, которая равна местной скорости звука. Можно дать и другую формулировку, принимая во внимание то обстоятельство, что в точке пересечения кривых на рис.14 проходит как кривая скорости потока, так и кривая скорости звука, а именно: критической скоростью звука называется такое значение местной скорости звука, которое равно скорости потока газа в данном месте. Как видим, в обоих случаях численное значение получится одним и тем же, поэтому безразлично, как именовать эту величину — критической скоростью или критической скоростью звука — и как обозначать ее: w_кр или а_кр. Более распространено название «критическая скорость» и обозначение а_кр.

Рассчитать критическую скорость можно по формуле

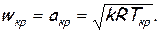(2.42)

где Т_кр — температура газа в критическом сечении. Последняя легко определяется с помощью уравнения энергии (2.19), левая часть которого записывается для сечения внутри резервуара (см. рис. 14), где w=0, Т=Т*, а правая часть — для критического сечения, в котором w_кр = а_кр, Т=Т_кр, а именно:

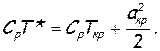
Заменив здесь 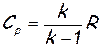и а_кр по формуле (2.42), получим после небольших преобразований

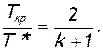(2.43)

Эта величина называется критическим отношением температур. Попутно запишем формулы для критического отношения давлений и для критического отношения плотносте й. Так как процесс течения газа через сопло идеальный, то связь между давлениями, плотностями и температурами устанавливается уравнением изоэнтропы (2.33) [5]. Тогда

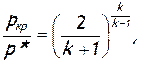(2.44)

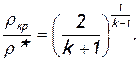(2.45)

Для воздуха эти соотношения имеют следующие значения:

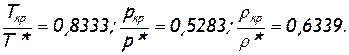
Определив из соотношения (2.43) температуру Т_кр и подставив ее значение в формулу (2.42), приходим к наиболее удобной формуле для расчета критической скорости

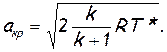(2.46)

Для воздуха 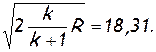. Следовательно,

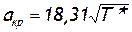м/сек. (2.47)

Установим связь между характерными скоростями w_mах, а_кр и а. Взяв отношение квадратов максимальной и критической скорости, получим

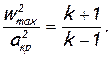(2.48)

Записав, далее, квадрат скорости звука

а² = kRТ,

выразим здесь температуру Т через температуру торможения Т*

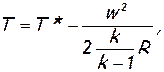
тогда

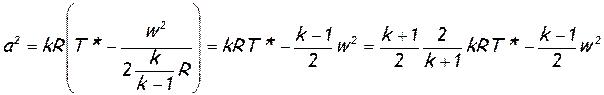
или

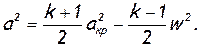(2.49)

По этим формулам и делается пересчет.

G Не напоминает Вам формула (2.49) теорему Пифагора? В любом случае постройте прямоугольный треугольник с катетами √ а² и √ (k-1)w²/2, и гипотенузой √ (k+1)a_кр²/2. Посмотрите внимательно на чертеж, подумайте и … Желаю успеха!

Температура торможения, критическая скорость и максимальная скорость являются величинами, так или иначе характеризующими полный запас энергии, которым обладает рассматриваемая единица массы газа. Если эта масса неподвижна, то ее полный запас энергии равен h* = c_рТ*, а этой величине пропорциональны квадрат критической скорости и квадрат максимальной скорости. Если рассматривается движущаяся масса газа, то ее полный запас энергии 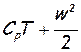путем введения температуры торможения легко приводится к C_рТ*.

Безразмерные скорости: число Маха (М), приведенные скорости λ и Λ.

Обычно скорость движения измеряется в метрах в секунду, километрах в час или каких-нибудь других единицах, имеющих размерность длина/время. Если же за единицу измерения скорости принять какую-либо из характерных скоростей, например скорость звука, то результат измерения будет выражаться безразмерным числом. В дальнейшем изложении будет ясно, что такой способ измерения скоростей является очень удобным.

Наиболее распространены три безразмерные скорости: число М, приведенная скорость λ и приведенная (относительная) скорость Λ. Приведенные скорости иначе называют коэффициентами скорости.

Числом М называется отношение скорости потока к местной скорости звука

M = w / a. (2.50)

Впервые эта величина была использована в трудах профессора Петербургской артиллерийской академии Н.В.Маиевского (1868), затем этим отношением пользовался австрийский физик Э.Мах (1887). В связи с этим в советской технической литературе отношение _ часто называют числом Маиевского, в немецкой — числом Маха. Иногда в английской литературе эту величину называют числом Бэрстоу.

Приведенной скоростью, или коэффициентом скорости λ называется отношение скорости потока к критической скорости

λ = w / a_кр. (2.51)

Числом Λ или относительной скоростью называется отношение скорости потока к максимальной скорости течения газа

Λ = w / w_max. (2.52)

Заметим, что величиной w²/w²_max = Λ² пользовался академик С.А. Чаплыгин еще в первых работах по газовой динамике. Поэтому ее иногда называют числом Чаплыгина.

Численное значение безразмерных скоростей может изменяться в следующем диапазоне:

число М от 0 до ∞

число λ от 0 до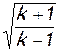

число Λ от 0 до 1,

так как скорость потока может изменяться от 0 до w_mах, а местная скорость звука в том сечении, где w=w_max, равна нулю (потому что температура равна нулю).

Связь между приведенными скоростями λ и Λ устанавливается следующим путем:

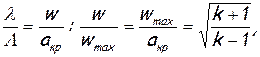
следовательно,

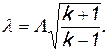(2.53)

Для установления зависимости между приведенной скоростью и числом М возьмем отношение их квадратов

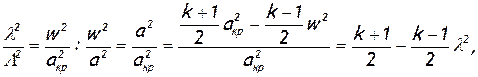
откуда

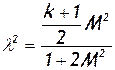(2.54)

или

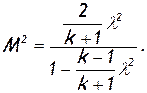(2.55)

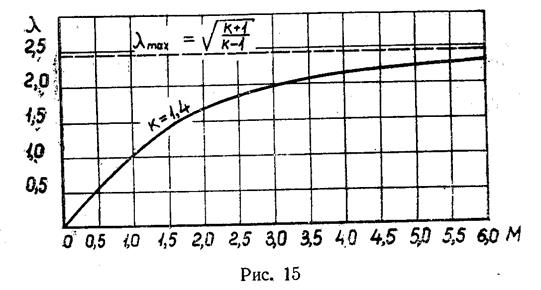
График зависимости приведенной скорости от числа М изображен на рис.15. Из графика видно, что значения М и λ численно совпадают при М=1 и М=0. Когда М−›∞, то приведенная скорость λ стремится ко вполне определенному пределу

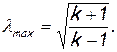
Это значение легко получить, устремив число М к бесконечности. Тогда w стремится к максимальной скорости и λ — к величине w_max / a_кр, которая равна 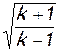(см. формулу (2.48)). Последняя является наибольшей из всех возможных величин λ и называется максимальной приведенной скоростью λ _мах. Для воздуха (k = 1,4) λ_max = 2,449.

Числа М, λ и Λ являются критериями подобия для сжимаемой жидкости. Так, например, если в двух геометрически подобных каналах числа М на входе будут одинаковы, то отношения скоростей, давлений, температур, плотностей в двух сечениях одного канала будут равны соответствующим отношениям в двух сходственных сечениях другого канала.

Поскольку число М связано с приведенными скоростями λ и Λ однозначными зависимостями, то, вместо того, чтобы устанавливать одинаковые числа М на входе в каналы, можно установить одинаковые числа λ или одинаковые числа Λ. В этом случае подобие потоков также будет соблюдаться.