Условие, при котором возможно восстановление сигнала без потерь, определяется из теоремы Котельникова [16,21].
Прямая формулировка теоремы Котельникова. Если сигнал 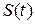 имеет финитную спектральную плотность, локализованную в полосе частот
имеет финитную спектральную плотность, локализованную в полосе частот 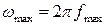 , то он может быть без потерь представлен дискретными отсчётами
, то он может быть без потерь представлен дискретными отсчётами 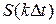 , удовлетворяющих условию:
, удовлетворяющих условию:
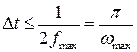 (4.2)
(4.2)
В зарубежной литературе теорему Котельникова чаще называют теоремой Найквиста или теоремой отсчётов.
Исходный сигнал в этом случае восстанавливается в следующем виде:
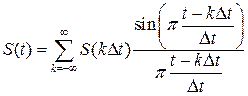 (4.3).
(4.3).
В общем случае, можно записать, что сигнал восстанавливается с помощью системы восстанавливающих функций:
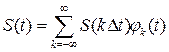
В случае теоремы Котельникова восстанавливающие функции имеют вид:
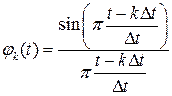
Пусть сигнал имеет вид 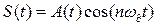 – согласно свойствам преобразования Фурье (см. раздел 2.5) для восстановления такого сигнала можно воспользоваться полосой частот шириной
– согласно свойствам преобразования Фурье (см. раздел 2.5) для восстановления такого сигнала можно воспользоваться полосой частот шириной 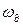 и со средней частотой
и со средней частотой 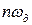 . В спектральной области такой полосе будут соответствовать две сдвинутые копии спектра
. В спектральной области такой полосе будут соответствовать две сдвинутые копии спектра 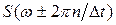 . Восстанавливающая функция будет иметь вид:
. Восстанавливающая функция будет иметь вид:
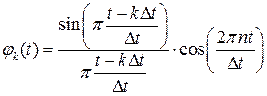 .
.
Обратная формулировка теоремы Котельникова/ Если f(x) задана в ограниченной области 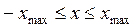 , то ее спектр F(ν) полностью определен набором отсчетов в точках, равноотстоящих друг от друга на расстоянии
, то ее спектр F(ν) полностью определен набором отсчетов в точках, равноотстоящих друг от друга на расстоянии 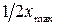 .
.
Поясним выбор шагов дискретизации по теореме Котельникова на рис. 4.2.
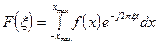 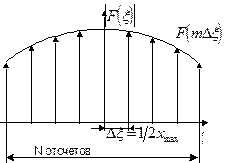
|
|
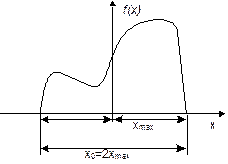
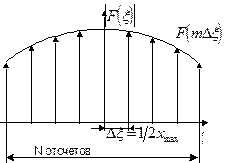
Рис.4.2. Выбор шага дискретизации по теореме Котельникова
При дискретизации согласно теореме Котельникова исходная функция f(x) может быть получена по ее дискретным значениям по формуле:
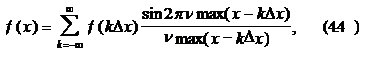 |
причем шаг дискретизации составляет
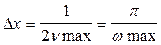 |
Однако согласно теории Фурье-анализа конечной апериодической функции f(x) соответствует бесконечный спектр и наоборот, конечный спектр соответствует бесконечной исходной функции.
Поэтому для реальных сигналов условия теоремы Котельникова в строгом смысле слова не выполняются.
1. Все реальные сигналы ограничены во времени и имеют неограниченный спектр, т.е. fв=µ.
2. В соответствии с рядом Котельникова восстановление осуществляется по бесконечному числу отсчетов (-µ £ k £ µ).
3. Поскольку сигнал восстанавливается по бесконечному числу отсчетов функций, то его восстановление осуществляется с бесконечной задержкой во времени.
Несмотря на эти недостатки, теорема Котельникова имеет фундаментальное значение, так как позволяет определить предельные возможности дискретной передачи сигналов.
Пример.
Передается речевой сигнал в полосе частот DF (от 0 до 3000 Гц). Время передачи Dt = 10 сек. Каждый дискретный отсчет кодируется 5 двоичными разрядами.
Определить минимальный объем памяти, требуемый для хранения информации Wзу.
T=1/2DF=1/6000=0,00016 с.,
следовательно, число отсчетов на интервале Dt:
N=Dt/T=10/0,00016=60000.
Объем ЗУ: Wзу =60000 ´ 5 = 300000 бит.
На практике теорему Котельникова для выбора шага дискретизации применяют следующим образом:
1. Определяют эффективную ширину спектра fэ.
2. Вычисляют шаг дискретизации T=1/2fэ.
3. На приемной стороне восстанавливается сигнал по следующей формуле
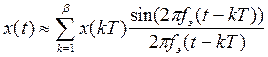 ,
,
где Т - длительность сигнала; Dt - шаг дискретизации; b =Dt/Т - база сигнала.
Итак, в результате дискретизации в соответствии с теоремой Котельникова от x(t) мы переходим к набору отсчетов или к вектору:
X = {xn}; 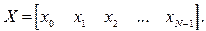 n=0, N-1.
n=0, N-1.
 2015-05-06
2015-05-06 1673
1673







