2015-05-06
1103
Одним из дискретных ортогональных преобразований, которое широко используется при сжатии цифровых изображений с потерями, является дискретное косинусное преобразование (ДКП). В частности, на использовании такого преобразования для сжатия изображений ориентирован широко распространенный стандарт JPEG, предложенный в 1985 году.
Основной этап процедуры сжатия цифровых изображений. заключается в преобразовании небольших блоков изображения при помощи двумерного ДКП. Обработка ведется блоками 8х8 пикселов. Выбор ДКП в качестве стандартного решения диктуется следующими причинами:
· Для изображений с сильно коррелированными отсчетами (коэффициент корреляции >0,7) эффективность ДКП в смысле компактности представления данных близка к преобразованию Карунена-Лоэва (это преобразование является оптимальным в том смысле, что оно ортонормированно и гарантирует некоррелированность коэффициентов преобразования – элементов яркости изображения Y).
· ДКП представляет собой ортогональное сепарабельное преобразование, независящее от изображения, поэтому его вычислительная сложность невелика.
|
|
|
 |
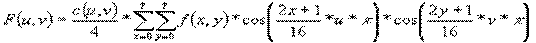Обработка каждой клетки выполняется независимо и заключается в выполнении ДКП по строкам и столбцам клетки, которое имеет вид:
(6.19)
В выражении (6.19) множитель C(u,v) является нормирующим и равен 1/Ö2 при u=0 или v=0 и равен единице для остальных значений индексов.
Общим недостатком дискретных ортогональных преобразований является их высокая вычислительная сложность. В связи с этим используются так называемые быстрые алгоритмы выполнения косинусного преобразования. Известные из литературы алгоритмы быстрых преобразований в базисах косинусных функций, хотя и отличаются меньшим числом операций умножения, но требуют дополнительных перекомпоновок после каждой итерации алгоритма. Одномерное косинусное преобразование может быть вычислено через одномерное преобразование Хартли [2]. При этом вначале производится перестановка элементов вектора исходных данных таким образом, что первую половину последовательности составляют нечетные элементы, а вторую половину последовательности - четные элементы в порядке возрастания номеров, а затем выполняется одномерное преобразование Хартли над модифицированным вектором [2]:
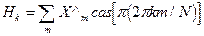
(где cas[...] = cos[....] + sin[...]), которое может быть вычислено по быстрому алгоритму; после чего выполняются дополнительные вычисления с элементами вектора результатов преобразования Хартли:
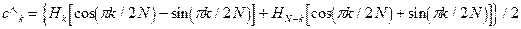(6.20)
где k = [1,...,N-1], причем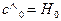 
.
Процедура обратного косинусного преобразования отличается от прямого алгоритма другой последовательностью вычислений - вначале выполняются преобразования, подобные выражению (6.20), после чего выполняется преобразование Хартли и лишь затем производится перестановка элементов вектора результатов.
|
|
|
К неудобствам косинусного преобразования следует отнести:
· неразделимость ядра преобразования для двумерного варианта;
· негибкие алгоритмы для различного размера ядра;
· несимметричный алгоритм обратного косинусного преобразования.
Заметим, что строго определяемое двумерное косинусное преобразование не обладает разделимым по координатам ядром, поэтому выполнение двумерного косинусного преобразования в целях сокращения объема вычислений может быть выполнено как модифицированное преобразование строчно-столбцовым методом, подобно тому, как поступают при выполнении двумерного преобразования Хартли [2].
В результате выполнения ДКП формируется 64 частотных компоненты фрагмента (или, что тоже, коэффициентов ДКП). В результате исходный фрагмент представлен в области пространственных частот. Этот шаг еще не приводит к сжатию изображения. Однако, при его выполнении полагается, что в подавляющем большинстве изображений близкие по своим координатам пикселы имеют и близкие значения. Поэтому, при переходе от фрагмента к его частотному представлению большая часть энергии сигнала сосредотачивается в области низких частот, т.е. компоненты с меньшим значением индекса k в выражении (6.20) имеют большие значения (см. рис. 6.1.).
При выполнении этой операции 64 исходных пикселов преобразуются в матрицу из 64 коэффициентов, которые характеризуют "энергию" исходных пикселов. Важнейшей особенностью этой матрицы коэффициентов является то, что первый коэффициент передает подавляющую часть "энергии", а количество "энергии", передаваемой остальными коэффициентами, очень быстро убывает. То есть, большая часть информации исходной матрицы 8х8 пикселов представляется первым элементом матрицы, преобразованной по способу ДКП.
На этом этапе происходит некоторая потеря информации, связанная с принципиальной невозможностью точного обратного преобразования (на этапе восстановления изображения). Однако эта потеря информации весьма незначительна по сравнению с потерями на следующем этапе.
 |
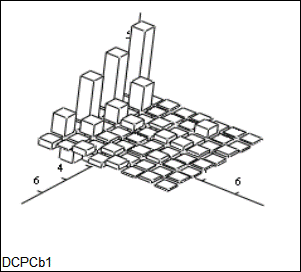Рис.6.1. Спектр ДКП отдельного фрагмента изображения
Преобразованная матрица из 64 пикселов затем проходит операцию квантования, которая применяется для сокращения разрядности коэффициентов. Процесс квантования, который ведет к сжатию коэффициентов ДКП, выражается следующим образом [11]:
zkl=round(ykl/qkl)=ë(ykl±ëqkl/2û)/qklû, k,l=0,1,...,7,
где qkl - весовой множитель матрицы квантования Q размера 8х8 с номером kl (ëxû обозначает наибольшее целое меньшее или равное x).
Иногда для формирования матрицы квантования может использоваться специальная весовая функция, позволяющая сформировать коэффициенты квантования, обращающие в 0 наибольшее число высоко и средне частотных коэффициентов. Согласно литературе [3,7], элементы матрицы Q линейно возрастают пропорционально сумме индексов элемента матрицы, например:
В результате квантования произошло обнуление многих коэффициентов ykl. Выбор матрицы Q определяется требуемым коэффициентом сжатия.
Именно здесь происходит самая значительная потеря информации - отбрасываются малые изменения коэффициентов. Поэтому в процессе восстановления изображения после операции обратного ДКП получаются уже другие параметры пикселов. Квантование также обеспечивает возможность последующего эффективного сжатия данных при помощи любого способа сжатия без потерь.
|
|
|
После квантования компоненты спектра всех обработанных фрагментов «вытягиваются» в последовательность чисел с помощью алгоритма диагонального сканирования. Схема обхода матрицы спектральных коэффициентов фрагмента показана на рис. 6.2. В основе такого сканирования лежит прием, позволяющий достичь большего уплотнения и основывающийся также на характерном виде спектра изображений реальных сцен.
Статистически доказано, что для реальных многоуровневых изображений двумерный квантованный спектр представляет собой матрицу треугольного вида. Большинство значений снизу и справа – нули. Построение элементов матрицы в цепочку производится так, как это показано на рис. 1.6. При этом в последовательность включаются только элементы от первого до последнего ненулевого. После него в последовательность включается специальный стоп – код. Это позволяет исключить из последовательности встречающиеся нули.
Далее обычно применяется метод однопроходного кодирования Хаффмана. Сначала анализируется вся последовательность символов. Часто повторяющимся сериям бит присваиваются короткие обозначения (маркеры). Различие размеров маркеров и представляемых ими битовых серий определяет достигаемую степень сжатия.
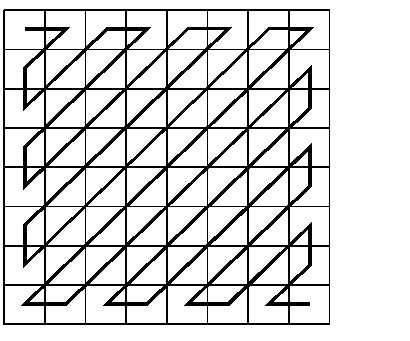
Рис. 6.2. Диагональное «зиг-заг» сканирование спектральных компонент
Восстановление. При восстановлении изображений перечисленные выше шаги выполняются в обратном порядке. Декодирование начинается с восстановления из полученного битового потока закодированных неравномерным кодом длин серий нулей и значащих элементов матрицы Z. Восстановление коэффициентов разложения Y^ по квантованным значениям Z выполняется по формуле
y^kl=z kl q kl (1.16)
 |
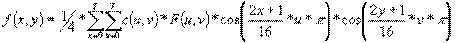Далее выполняется обратное ДКП:
После этого цветовое пространство данных изображения можно преобразовать в исходный вид. Потери при обратном ДКП также не велики по сравнению с потерями квантования.
|
|
|
Коэффициент архивации в JPEG может изменятся в пределах от 2 до 200 раз (на практике коэффициент сжатия не превосходит 20-25) [11].
