Выполнение фильтрации в частотной области

Идея частотной фильтрации основана на отличии спектров полезного сигнала и помехи [5,21]. При этом используются линейные частотные фильтры, позволяющие подавлять помеху и улучшать тем самым соотношение сигнал/помеха. Параметры фильтра определяются спектральными характеристиками сигнала и помехи. На практике наиболее часто встречаются следующие случаи.

1) На вход фильтра поступает узкополосный сигнал и широкополосная помеха. В этом случае эффективен узкополосный фильтр с полосой пропускания Dw_х;

2) На вход фильтра поступает широкополосный сигнал и узкополосная помеха с шириной спектра Dw_r. Для подавления подобной помехи фильтр должен обеспечивать подавление помехи в полосе Dw_r;

3) На вход фильтра поступают периодический сигнал и широкополосная помеха.

Рассмотрим случай, когда полезный сигнал является гармоническим, а помеха типа белого шума. Для выделения полезного сигнала в этом случае должен быть использован узкополосный фильтр, настроенный на частоту сигнала. Отношение мощности сигнала к мощности помехи на выходе фильтра при этом

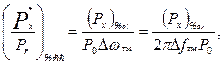(6.26)

где Р₀ - средняя мощность помехи, приходящаяся на единицу полосы; Dw_ф - полоса пропускания фильтра. Как видно из выражения (6.26), отношение 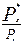можно сделать сколь угодно большим за счет уменьшения полосы пропускания фильтра Df_ф.

В реальных условиях полезный сигнал поступает лишь в течении определенного времени Т_х и, следовательно, его спектр неограничен.

Известно, что практическая ширина спектра такого сигнала связана с его длительностью соотношением

Df_фТ_х=m, (6.27)

где m - постоянная, зависящая от формы сигнала. Обычно принимается m @ 1.

Длительность сигнала Т_х должна быть выбрана такой, чтобы его спектр был не шире полосы пропускания фильтра Df_х£Df_ф.

Подставляя в (6.27) вместо Df_ф величину Df_х, получаем

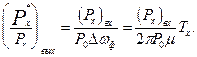(6.28)

Формула (6.28) показывает, что увеличение отношения сигнал/помеха достигается за счет увеличения длительности сигнала Т_х, т.е. времени наблюдения.

Таким образом, при частотной фильтрации улучшение отношения сигнал/помеха окупается ценой увеличения времени наблюдения сигнала.

Кроме указанных видов фильтров в частотной области может выполняться линейная фильтрация более общего вида, описываемая выражением типа свертки. Схема выполнения фильтрации сигнала в частотной области приведена на рис. 6.6. Обобщенно подобный метод частотной фильтрации иногда называют операционной частотной фильтрацией. Таким методом можно выполнять заданные математические преобразования исходного сигнала, например, дифференцирование или интегрирование [21, 25].

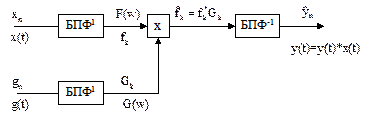
Рис.6.6. Схема операционной частотной фильтрации

Согласованные фильтры предназначены для выделения сигналов известной формы на фоне шумов. Критерием оптимальности таких фильтров является получение на выходе максимально возможного отношения амплитудного значения сигнала к действующему значению помехи [25]. Реакция согласованного фильтра эквивалентна действию корреляционного приемника. Схема выполнения согласованной фильтрации приведена рис. 6.7.

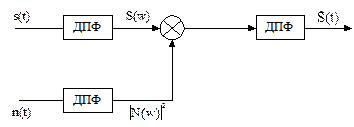
Рис. 6.7. Схема выполнения согласованной фильтрации

Для выделения известного сигнала S(t) из стационарного шума n(t) оптимальным является фильтр с передаточной функцией [21, 28]:

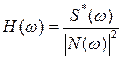(6.29)

S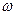^{(*) ­­­} () - сопряженный спектр Фурье (или Фурье образ) исходного сигнала, 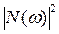- спектральная плотность шума, ω=2πν. Этот фильтр носит название согласованного фильтра.

Если нужно минимизировать среднеквадратичную ошибку восстановленного сигнала, то:

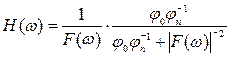(6.30)

где 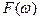- спектр сигнала; 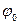- спектр мощности восстанавливаемого сигнала, 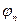- спектр мощности шума.

При отсутствии шума для минимизации среднеквадратичной погрешности используется инверсный фильтр [28]:

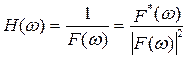(6.31)