Таким образом, в основе работы не рекурсивного фильтра лежит вычисление свертки вектора исходных данных
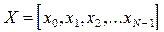
и импульсной характеристики фильтра (ядра свертки)
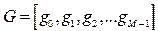 ,
,
где 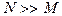 . Подобные вычисления могут быть вычислены как на основе прямого алгоритма (см. раздел 1.7), так и через спектральные дискретные преобразования Фурье и Хартли (см. разделы 6.1 и 6.2). Возникает естественный вопрос, какой метод предпочтителен, исходя из меньшего объёма вычислений, а следовательно, и времени, необходимого для реализации данного метода.
. Подобные вычисления могут быть вычислены как на основе прямого алгоритма (см. раздел 1.7), так и через спектральные дискретные преобразования Фурье и Хартли (см. разделы 6.1 и 6.2). Возникает естественный вопрос, какой метод предпочтителен, исходя из меньшего объёма вычислений, а следовательно, и времени, необходимого для реализации данного метода.
Если размер “окна” или ядра свёртки равен 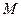 , а длина вектора исходных данных, то для получения
, а длина вектора исходных данных, то для получения 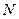 отсчётов результата апериодической свёртки необходимо выполнить:
отсчётов результата апериодической свёртки необходимо выполнить:
Qсв = MN (БО), (8.27)
где БО – базовая операция, включающая операцию умножения и сложения действительных чисел. Сложность БО составляет:
qБО = qумн + qсл.
Отсюда можно получить, что время вычисления свертки по прямому алгоритму
Tсв = Qсв *Δt = MN(qумн + qсл) *Δt
где Δt - длительность такта В.У.
При этом необходимо отметить, что задаваемые данные и результаты являются действительными числами, т.е. при расчёте прямого алгоритма 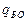 определяется суммой операций умножения и сложения действительных чисел.
определяется суммой операций умножения и сложения действительных чисел.
При вычислении свёртки на основе спектрального преобразования выполняются следующие действия:
1. Прямые спектральные преобразования Фурье или Хартли исходного вектора.
2. При вычислении свёртки на основе ДПХ выполняются перекомпоновка полученного спектра (см. раздел 6.2, т.е. формируется 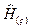 и вычисляются
и вычисляются 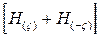 и
и 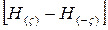 .
.
3. Поэлементное перемножение спектров для ДПФ: 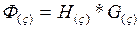 или вычисление в
или вычисление в 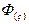 согласно методике в разделе 2.2 - для ДПХ.
согласно методике в разделе 2.2 - для ДПХ.
4. Обратное преобразование для функции 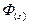 на основе ДПФ или ДПХ.
на основе ДПФ или ДПХ.
Таким образом, если свёртка при 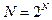 вычисляется через ДПФ на основе быстрых алгоритмов:
вычисляется через ДПФ на основе быстрых алгоритмов:
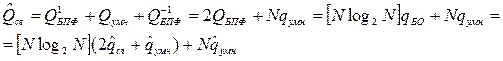 (8.28)
(8.28)
где 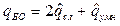
При расчёте 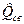 свёртки необходимо учитывать, что
свёртки необходимо учитывать, что
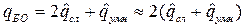 ,
,
где 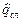 и
и 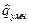 - сложность операций сложения и умножения комплексных чисел, причём
- сложность операций сложения и умножения комплексных чисел, причём
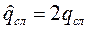
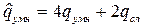
аналогичных действий с действительными числами, т.е.
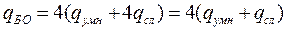
Тогда получим
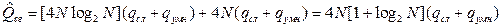 (8.29)
(8.29)
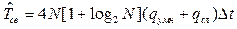
Отсюда нетрудно получить с учетом выражения (8.27), что прямой метод вычисления свёртки предпочтителен, если:
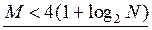 (8.30)
(8.30)
Из (8.30) следует, например, что для 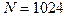 предельный размер
предельный размер 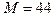 для вычисления по прямому алгоритму, а для
для вычисления по прямому алгоритму, а для 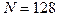 предельный размер окна составляет
предельный размер окна составляет 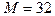
Если свёртка вычисляется на основе БПХ, то при том же числе БО их сложность умножается:
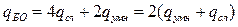
для действительных чисел, однако требуется выполнить операции по вычислению функции 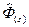 , что потребует примерно
, что потребует примерно 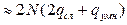 . С учетом сложности базовых операций при прямом и спектральном алгоритме можно получить, что прямой алгоритм предпочтительнее алгоритма вычисления свертки через БПХ, если:
. С учетом сложности базовых операций при прямом и спектральном алгоритме можно получить, что прямой алгоритм предпочтительнее алгоритма вычисления свертки через БПХ, если:
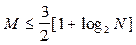 (8.31)
(8.31)
Что же касается БДОП типа Уолша - Адамара, то базис этих функций для вычисления свёртки мало пригоден, поскольку в отличии от ДПХ для подобных преобразований нет простых формул для связи с ДПФ и не справедлива теорема о свёртке. Известны алгоритмы вычисления свёртки и на основе указанных ДОП [18, 19], однако отсутствие операции умножения при выполнении БДОП не компенсируется сложностью вычисления 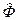 .
.
 2015-05-06
2015-05-06 813
813








