2015-05-06
1115
Как уже отмечалось в разделе 6.2, множители ядра преобразования Харли не обладают свойством мультипликативности. Это не позволяет достаточно просто записать выражения для итерации алгоритма БПХ в матричной форме.
Выполним выкладки для получения выражений, описывающих итерацию БПХ. Для этого возьмем за основу выражения для описания “бабочки” БПФ (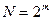
) произвольной итерации согласно (8.10):
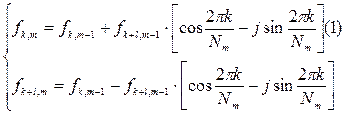(8.20)
здесь l=2m-1,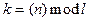 
, .
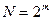Воспользуемся выражениями, связывающими отсчёты ДПФ и ДПХ [3]:
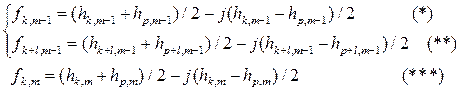
подставим (*), (**) и (***) в формулу (1) выражения (8.20) и получим:
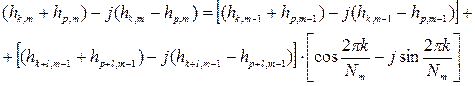(8.21)
 |
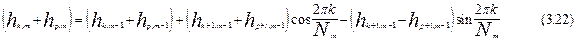В свою очередь, из выражения (8.21) можно получить выражения для действительной и мнимой частей:
 |
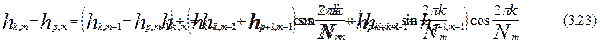Сложив выражения (3.22) и (3.23), можно получить:
Заметим, что (p+l)mod lºp, откуда следует:
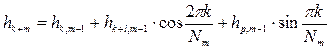(8.24)
 |
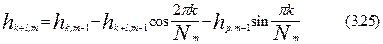Проделав аналогичные выкладки, можно получить, что:
здесь p = l+(l-k)mod l,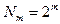 
, 
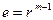, k=(n)mod l, n - текущий индекс элемента вектора (
).
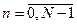Таким образом, при 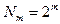“бабочка” БПХ подобна “бабочке” БПФ, но обладает следующим отличием: правило вычисления индекса элемента синусной компоненты иное, чем у индекса косинусного элемента. Индекс же элемента косинусной компоненты и “свободной” компоненты, а также индекса у результирующего элемента и аргументы косинуса и синуса вычисляются так же, как и для “бабочки” БПФ [23].
|
|
|
На рис. 8.7. приведен граф базовой операции бабочка для алгоритма БПХ.
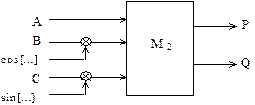
Рис.8.7. Граф базовой операции БПХ, где
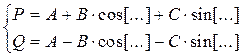
Граф алгоритма БПХ для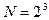 
приведен на рис.8.8.
 |
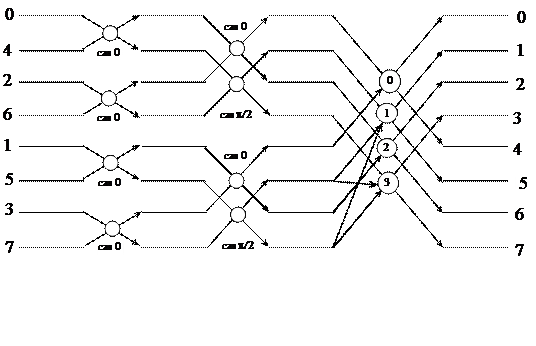Рис.8.8. Граф алгоритма БПХ
Из представленного графа видно, что на третьей итерации при вычислени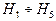и 
и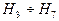 
в “бабочках” участвуют cos[...] и sin[...] компоненты с разными элементами.
