Рассмотрим вначале алгоритмы БПФ для 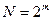 с прореживанием по времени.
с прореживанием по времени.
Такой алгоритм является итерационным и включает 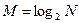 итераций,
итераций,
причем на каждой стадии выполняется N/2 базовых операций вида (7.11), откуда нетрудно получить, что общая трудоемкость алгоритма БПФ [21]:
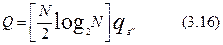
где qБО - сложность базовой операции.
В свою очередь, базовая операция требует для своего выполнения 1 операцию умножения и 2 операции сложения комплексных чисел или, в пересчете на операции с действительными числами, 4 операции умножения и 4 операции сложения действительных чисел.
Для ЭВМ предыдущих поколений, где операции умножения выполнялись главным образом программным (а не аппаратным) способом, особую важность имело прежде всего сокращение числа операций умножения как наиболее длительных.
В современных ЭВМ эта задача не столь актуальна, так как длительность практически всех операций близка, особенно в специализированных процессорах.
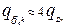 |
Поэтому будем полагать, что сложность базовой операции при работе с комплексными числами равна
где qD=qx+q+
Здесь и далее под q подразумевает сложность отдельной машинной команды, например, в числе тактов работы процессора, необходимой для выполнения конкретной арифметической операции. Следовательно, для БПФ сложность алгоритма можно определить как:
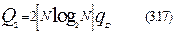 |
При обработке вектора данных длиной
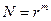 на каждой из M итераций выполняется по N/r базовых операций, т.е.
на каждой из M итераций выполняется по N/r базовых операций, т.е.
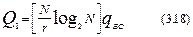 |
Однако сложность базовой операции, как это можно видеть из (8.15), составит:
qБО»r2qk
где qk=qУМН+qСЛ - для комплексных чисел, или, как и в случае 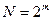 , посчитаем, что qk=4qD и получим, подставив в (8.15) значения
, посчитаем, что qk=4qD и получим, подставив в (8.15) значения 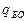 :
:
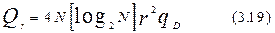 |
В таблице 8.1 приведены значения для времени выполнения ДПФ и БПФ по различным основаниям при условии, что tсл=tумн=100нсек.
Таблица 8.1.
| Размер вектора N | Время выполнения, сек. | ||
| БПФ | ДПФ | ||
| 24 | 2,56×10-5 | 2,0×10-4 | |
| 52 | 2×10-4 | 5×10-4 | |
| 33 | 6,5×10-5 | 6,5×10-5 | |
| 25 | 6,4×10-5 | 8×10-4 | |
| 34 | 7,8×10-4 | 5,3×10-3 | |
| 53 | 1,5×10-3 | 1,2×10-3 | |
| 27 | 3,6×10-4 | 1,3×10-2 | |
| 29 | 1,8×10-3 | 2×10-1 | |
| 54 | 10-2 | 3×10-1 | |
| 216 | 4,1×10-3 | 8,3×10-1 | |
| 214 | »1 сек. | »36 мин. |
Поэтому с точки зрения сокращения вычислительных затрат выгодны алгоритмы БПФ по основанию 2 (или 4), причем с ростом основания r выигрыш уменьшается.
8.7. Выполнение БПФ для случаев 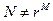
Если 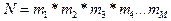 , то в этом случае выполняется алгоритм БПФ по смешанному основанию. Он может быть реализован как алгоритм с прореживанием по частоте или как алгоритм с прореживанием по времени. В обоих случаях такой алгоритм выполняется за
, то в этом случае выполняется алгоритм БПФ по смешанному основанию. Он может быть реализован как алгоритм с прореживанием по частоте или как алгоритм с прореживанием по времени. В обоих случаях такой алгоритм выполняется за 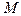 итераций. Однако на каждой итерации выполняется различное число базовых операций, причём размерность матрицы ядра ДПФ базовой операции на каждой итерации различна и составляет
итераций. Однако на каждой итерации выполняется различное число базовых операций, причём размерность матрицы ядра ДПФ базовой операции на каждой итерации различна и составляет 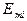 , а число БО соответственно на каждой итерации составляет -
, а число БО соответственно на каждой итерации составляет - 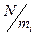 , где до первой итерации элементы вектора переупорядочиваются с шагом
, где до первой итерации элементы вектора переупорядочиваются с шагом 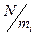 [8]. На рис. 8.5. приведен в качестве примера граф БПФ для N = 6 = 3x2.
[8]. На рис. 8.5. приведен в качестве примера граф БПФ для N = 6 = 3x2.
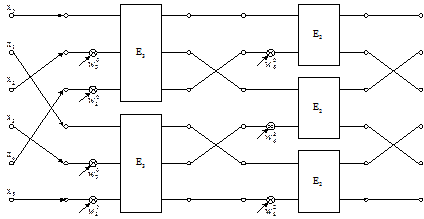
Рис.8.5. Граф БПФ для N=6
Если же 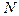 является простым числом и не может быть разложено на взаимно-простые множители, то в этом случае также можно использовать алгоритм быстрого преобразования, но особого вида - так называемый алгоритм Винограда [15]. Этот алгоритм позволит значительно сократить число операций умножения, но зато число операций сложения сокращается не столь существенно, причем требуются достаточно сложные процедуры перекомпоновки векторов промежуточных результатами.
является простым числом и не может быть разложено на взаимно-простые множители, то в этом случае также можно использовать алгоритм быстрого преобразования, но особого вида - так называемый алгоритм Винограда [15]. Этот алгоритм позволит значительно сократить число операций умножения, но зато число операций сложения сокращается не столь существенно, причем требуются достаточно сложные процедуры перекомпоновки векторов промежуточных результатами.
Поэтому для современных ЭВМ, и особенно спецпроцессоров, когда 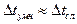 (а в некоторых из них одинаково время любой операции), такие алгоритмы, как и БПФ по смешанному основанию, не приносят слишком большого выигрыша по времени.
(а в некоторых из них одинаково время любой операции), такие алгоритмы, как и БПФ по смешанному основанию, не приносят слишком большого выигрыша по времени.
С точки зрения экономии времени целесообразно дополнить вектор до 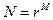 (желательно
(желательно 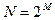 или
или 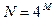 ) нулями. Однако такой прием приводит к некоторому искажению результата, что связано с введением так называемой оконной функции. Пусть исходных сигнал задан в виде вектора из N1 отсчетов (рис.8.6.).
) нулями. Однако такой прием приводит к некоторому искажению результата, что связано с введением так называемой оконной функции. Пусть исходных сигнал задан в виде вектора из N1 отсчетов (рис.8.6.).
Для того, чтобы иметь возможность использовать алгоритмы БПФ дополним сигнал нулевыми отсчетами до общего числа отсчетов N= 2M, причем N – ближайшее большее к N1 .В этом случае исходный сигнал оказывается заданным с помощью функции
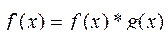 ,
,
где g(x) – функция окна вида
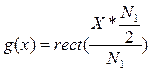
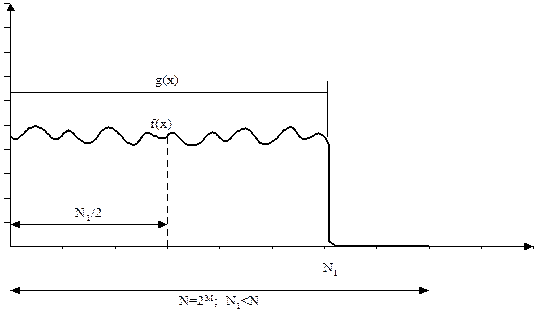 Рис. 8.6. Проявление эффекта окна
Рис. 8.6. Проявление эффекта окна
|
Поэтому при вычислении преобразования Фурье от 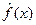 проявляется эффект, получивший название “эффекта окна”.
проявляется эффект, получивший название “эффекта окна”.
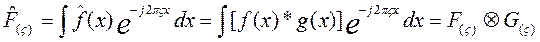 ,
,
где 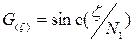 при этом функция
при этом функция 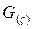 будет тем ближе к
будет тем ближе к 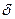 - функции, чем шире
- функции, чем шире 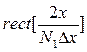 или чем
или чем 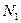 ближе к N. Проявляется “эффект окна” в искажении периферийных областей спектра сигнала [21]. Поэтому, во избежание проявления “эффекта окна” удобнее функцию
ближе к N. Проявляется “эффект окна” в искажении периферийных областей спектра сигнала [21]. Поэтому, во избежание проявления “эффекта окна” удобнее функцию 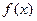 при переходе от
при переходе от 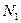 к
к 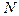 сделать периодической с периодом
сделать периодической с периодом 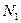 , дополнив вектор исходных данных до длины
, дополнив вектор исходных данных до длины 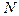 , повторив первые
, повторив первые 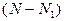 отсчетов за последние элементы вектора
отсчетов за последние элементы вектора 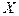 .
.
 2015-05-06
2015-05-06 1443
1443
