2015-05-06
292
Пусть система состоит из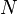 
материальных точек с массами 
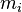и радиус-векторами 
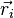. Как известно[1][3], центром масс (центром инерции) системы материальных точек называется геометрическая точка, радиус-вектор 
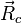которой удовлетворяет равенству
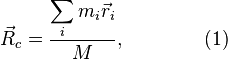
где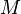 
— масса всей системы, равная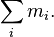 
Дифференцируя (1) два раза по времени, для ускорения центра масс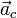 
получаем:
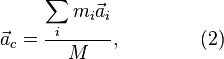
где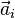 
— ускорение материальной точки с номером i.
Для последующего рассмотрения целесообразно разделить все силы, действующие на тела системы, на два типа:
· Внешние силы — силы, действующие со стороны тел, не входящих в рассматриваемую систему. Равнодействующую внешних сил, действующих на материальную точку с номером i обозначим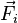 
.
· Внутренние силы — силы, с которыми взаимодействуют друг с другом тела само́й системы. Силу, с которой на точку с номером i действует точка с номером k, будем обозначать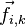 
. Соответственно, сила воздействия i -й точки на k -ю точку будет обозначаться 
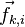. Из сказанного очевидно, что если 
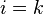, то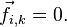 
Используя введённые обозначения, второй закон Ньютона для каждой из рассматриваемых материальных точек можно записать в виде
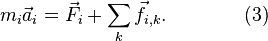
Суммируя все уравнения вида (3), получим:
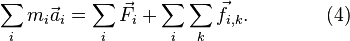
Выражение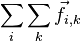 
представляет собой сумму всех внутренних сил, действующих в системе. Учтём теперь, что по третьему закону Ньютона в этой сумме каждой силе 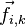соответствует сила 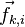такая, что 
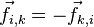и, значит, выполняется 
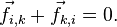Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, из (4) следует
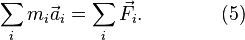
Далее, обозначив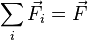 
и подставив полученное выражение в (2), приходим к уравнению
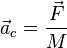или к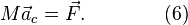 
Таким образом, движение центра масс определяется только внешними силами, а внутренние силы никакого влияния на это движение оказать не могут. Формула (6) является математическим выражением теоремы о движении центра масс системы.
