Сначала рассмотрим случай одной материальной точки. Пусть  — масса материальной точки М,
— масса материальной точки М,  — ее скорость,
— ее скорость,  — количество движения.
— количество движения.
Выберем в окружающем пространстве точку О и построим момент вектора  относительно этой точки по тем же правилам, по которым в статике вычисляется момент силы. Получим векторную величину
относительно этой точки по тем же правилам, по которым в статике вычисляется момент силы. Получим векторную величину
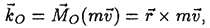
которая называется моментом количества движения материальной точки относительно центра О (рис. 31).
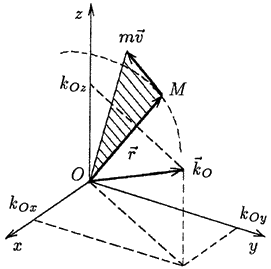
Рис. 31.
Построим с началом в центре О декартову прямоугольную систему координат Oxyz и спроектируем вектор ко на эти оси. Его проекции на эти оси, равные моментам вектора  относительно соответствующих координатных осей, называются моментами количества движения материальной точки относительно координатных осей:
относительно соответствующих координатных осей, называются моментами количества движения материальной точки относительно координатных осей:
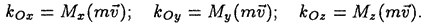
Пусть теперь имеем механическую систему, состоящую из N материальных точек  . В этом случае момент количества движения можно определить для каждой точки системы:
. В этом случае момент количества движения можно определить для каждой точки системы:
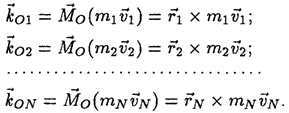
Геометрическая сумма моментов количеств движения всех материальных точек, входящих в состав системы, называется главным моментом количеств движения или кинетическим моментом системы:
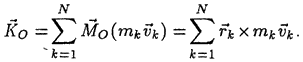
Проекции кинетического момента системы на координатные оси
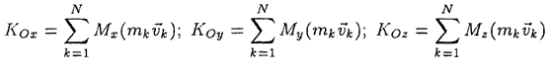
называются кинетическими моментами относительно координатных осей.
 2015-05-06
2015-05-06 362
362








