Тема: Применение теоремы об изменении кинетической энергии к исследованию движения механической системы».
Механическая система под действием сил тяжести приходит в движение из состояния покоя. Учитывая трение скольжения груза 1, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорости движения всех тел, входящих в механическую систему в тот момент времени, когда пройденный грузом путь станет равным S. Начальное положение системы показано на рисунке 6.
Дано:
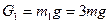 ;
; 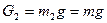 ;
; 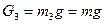 ;
; 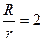 ;
; 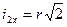 ; S=S1=1м; f=0,1
; S=S1=1м; f=0,1
Покажем на механической системе веса тел 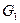 ,
, 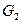 ,
, 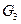 ; линейные скорости
; линейные скорости 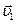 ,
, 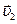 ,
, 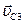 угловые скорости
угловые скорости 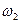 ,
, 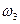 ; силу трения груза 1
; силу трения груза 1 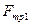 Расчетная схема данной механической системы изображена на рисунке 6.
Расчетная схема данной механической системы изображена на рисунке 6.
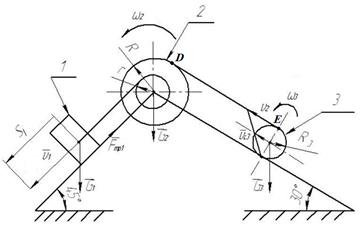
Рис. 6
Для решения применим теорему об изменении кинетической энергии системы в интегральном виде:
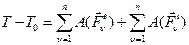 ,
,
где 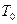 и
и 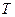 - кинетическая энергия системы в ее начальном и конечном
- кинетическая энергия системы в ее начальном и конечном
положениях;
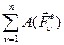 - сумма работ внешних сил, приложенных к системе;
- сумма работ внешних сил, приложенных к системе;
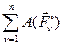 - сумма работ внутренних сил системы.
- сумма работ внутренних сил системы.
Для рассматриваемой системы, состоящей из абсолютно твердых тел, соединенных нерастяжимыми нитями:
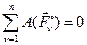 .
.
Так как в начальном положении система находится в покое, то 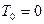 .Из этого следует, что уравнение примет вид:
.Из этого следует, что уравнение примет вид:
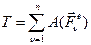 . (1)
. (1)
Кинетическая энергия рассматриваемой системы T в конечном ее положении равна сумме кинетических энергий тел 1, 2, 3:
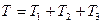 . (2)
. (2)
Кинетическая энергия груза 1, который движется поступательно:
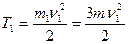 . (3)
. (3)
Кинетическая энергия блока 2, с заданным радиусом инерции, совершающего вращательное движение:
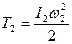 ; (4)
; (4)
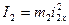 . (5)
. (5)
Запишем соотношения между скоростями и перемещениями для механической системы:
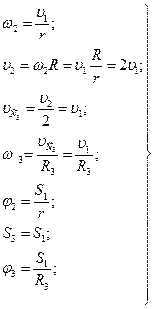 (6)
(6)
где: 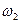 ,
, 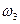 - угловые скорости тел;
- угловые скорости тел;
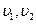 - линейные скорости точек тел (
- линейные скорости точек тел (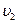 - скорость точки Д барабана равна скорости точки Е катка);
- скорость точки Д барабана равна скорости точки Е катка);
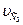 - скорость центра масс однородного катка 3;
- скорость центра масс однородного катка 3;
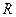 ,
, 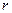 ,
, 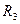 - радиусы тел 2 и 3.
- радиусы тел 2 и 3.
Используя уравнение взаимосвязи между параметрами (6), получаем:
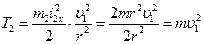 . (7)
. (7)
Кинетическая энергия сплошного однородного цилиндра 3, совершающего плоское движение, складывается из энергии поступательного движения 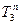 центра тяжести катка и энергии его вращательного движения
центра тяжести катка и энергии его вращательного движения 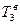 :
:
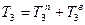 . (8)
. (8)
Определим энергию поступательного движения цилиндра 3, используя уравнения (6):
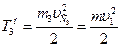 . (9)
. (9)
Определим энергию вращательного движения цилиндра 3, используя уравнения (6):
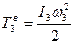 . (10)
. (10)
Момент инерции для сплошного однородного цилиндра 3 равен:
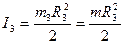 ; (11)
; (11)
Тогда:
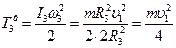 . (12)
. (12)
Кинетическая энергия механической системы будет равна сумме кинетических энергий всех материальных точек, входящих в систему:
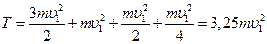 (13)
(13)
Далее запишем сумму работ всех внешних сил, действующих на механическую систему. Ее составляет работа сил тяжести каждого тела 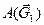 ,
, 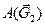 ,
, 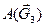 и работа силы трения груза 1
и работа силы трения груза 1 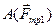 .
.
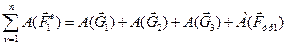 . (14)
. (14)
Работа груза 1 равна:
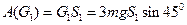 . (15)
. (15)
Работа силы веса блока 2 будет равна нулю, так как блок 2 не совершает никаких перемещений:
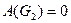 .
.
Учитывая уравнение связи, получаем, что работа силы веса однородного цилиндра 3 равна:
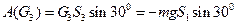 . (16)
. (16)
Работа силы трения груза 1 равна:
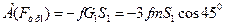 . (17)
. (17)
Сумма работ всех внешних сил механической системы равна:
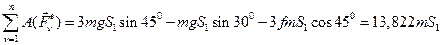 . (18)
. (18)
Так как:
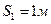 , то:
, то:
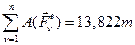 .
.
Подставим результаты уравнений в уравнение и получим:
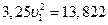 .
.
Выразим скорость груза 1 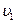 :
:
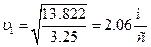 .
.
 2015-05-06
2015-05-06 1551
1551








