1) изобразить схематически механическую систему, равновесие которой рассматривается, и все активные силы. включая силу трения, показать на чертеже;
2) согласно принципу освобождаемости от связей, отбросить связи и заменить их реакциями связей;
3) выбрать обобщенную координату, сообщить системе виртуальное перемещение, написать выражение для виртуальной работы (или обобщенной силы) и, приравняв ее нулю, определить искомые величины.
Пример решения задач по теме:
Задача.
Составная балка АD, лежащая на четырех опорах А, В, С, D, состоит из трех балок AM, MN, ND, шарнирно соединенных в точках М и N. К балке приложены сосредоточенные нагрузки Р1=250 Н, Р2=300 Н, Р3=500 Н. Размеры балки показаны на рисунке 7. Определить реакцию опоры в точке С.
Запишем условия в краткой материальной форме:
Дано: Р1=250Н, Р2=300Н, Р3=500Н
Определить: RC
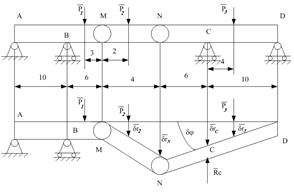
Рис.7
Решение:
Мысленно отбросим опору в точке С и заменим ее реакцией 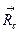 (рис. 7). Система приобретает одну степень свободы. Даем системе возможное перемещение в точке С в направлении
(рис. 7). Система приобретает одну степень свободы. Даем системе возможное перемещение в точке С в направлении 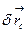 . Обозначим через
. Обозначим через 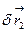 и
и 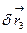 перемещение точек приложения сил
перемещение точек приложения сил 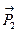 и
и 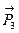 и через
и через 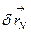 - перемещение точки N.
- перемещение точки N.
Так как система находиться в равновесии, то 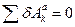 , то есть:
, то есть:
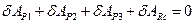 ,
,
где 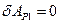 - так как нет перемещения точки приложения силы
- так как нет перемещения точки приложения силы 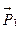 ,
,
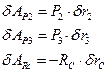
Определим зависимости между перемещениями:
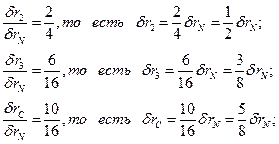
Таким образом, получаем:
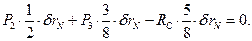
Так как 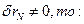
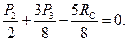
Откуда:
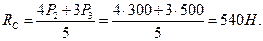
 2015-05-06
2015-05-06 350
350








