Задача 1. На горизонтальный вал насажен однородный диск А радиусом R и массой m1

На горизонтальный вал насажен однородный диск А радиусом R и массой m₁. На диск намотана нить, к концу которой подвешен груз В с массой m₂. Пренебрегая трением в подшипнике вала, определить угловую скорость диска А в момент t₁ после начала движения, если груз В движется из состояния покоя.

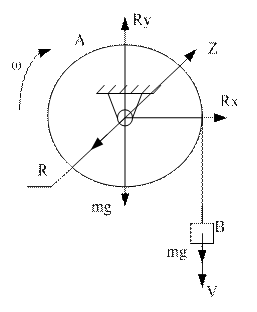
Рис.5

Решение:

Запишем условия в краткой математической форме:

Дано: m₁, m₂, R, t₁,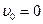

Определить: ω₁

Рассмотрим движение системы: диск А и груз В.

К системе приложены вешние силы: вес диска 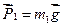, вес груза 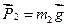, составляющие реакции в подшипнике .

Воспользуемся теоремой об изменении кинетического момента относительно оси вращения:

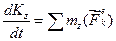(1)

Кинетический момент системы относительно оси вращения z:

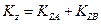(2)

Кинетический момент диска:

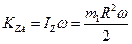(3)

Кинетический момент груза:

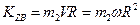(4)

Таким образом:

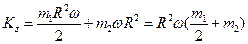(5)

Далее определим сумму моментов всех внешних сил относительно оси z:

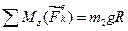(6)

Подставляя в исходное уравнение найденные значения кинетического момента 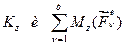, получим:

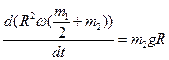(7)

Выражение (7) представляет собой дифференциальное уравнение первого порядка с разделяющимися переменными. Разделяя переменные и интегрируя, получим

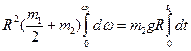(8)

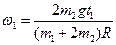(9)

Таким образом, диск вращается равноускоренно.