2015-05-06
317
Плоское движение твердого тела можно представить как сумму двух движений: поступательного – вместе с центром масс и вращательного – вокруг центра масс. Отсюда следует, что для описания плоского движения необходимо описать движение его центра масс, а для этого можно использовать теорему о движении центра масс (38) в проекции на плоскость движения (Oxy):
; 
.
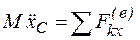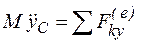Для описания вращательной составляющей плоского движения можно использовать теорему об изменении момента количества движения системы в относительном движении по отношению к центру масс, которая имеет вид, аналогичный (44):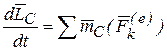 
, или в проекции на ось перпендикулярную плоскости движения:
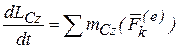. (48)
Учитывая, что (45):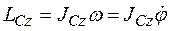 
, находим 
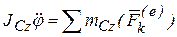. Таким образом, получили три уравнения, которые и называются дифференциальными уравнениями плоского движения:
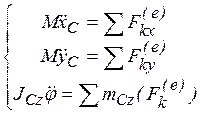(49)
