2015-05-06
366
При поступательном движении все точки тела двигаются одинаково, поэтому для описания поступательного движения твердого тела достаточно описать движение хотя бы одной его точки. Если в качестве этой точки выбрать центр масс тела (т. С), то для этого можно использовать теорему о движении центра масс (38) или в проекции на оси координат:
; 
; 
.
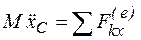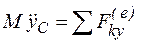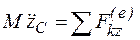Для описания вращательного движения воспользуемся теоремой об изменении момента количества движения системы (44) в проекции на ось z (ось вращения):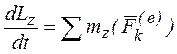 
. Кинетический момент твердого тела относительно оси вращения найдем по формуле (45). В результате получим: 
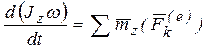. Поскольку момент инерции тела – величина постоянная: Jz = const, то, вынеся его за знак производной, получим 
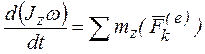или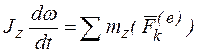 
– это и есть дифференциальное уравнение вращательного движения твердого тела. Поскольку 
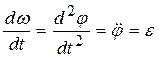- угловое ускорение, то это уравнение можно записать в виде: 
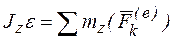или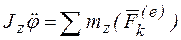 
. Можно заметить, что это уравнение по своей структуре аналогично основному уравнению динамики (1). При его решении могут возникнуть две задачи динамики: прямая и обратная.
