Вытекание идеальной жидкости из отверстия

ИЗУЧЕНИЕ ЗАКОНОВ ДИНАМИКИ ЖИДКОСТИ

КРАТКАЯ ТОРИЯ

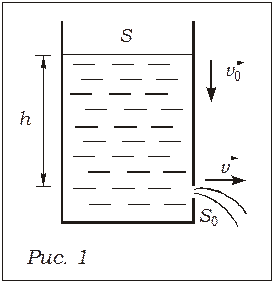Рассмотрим цилиндрический сосуд с отверстием, в которое может быть вставлена трубка (рис. 1). Определим зависимость скорости 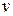вытекания жидкости из отверстия (трубки) от высоты 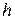ее свободной поверхности, а также зависимость высоты 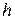от времени.

Вытекание идеальной жидкости из отверстия

Запишем уравнение Бернулли для сечений отверстия 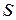и сосуда 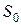(рис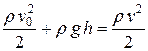. 1):

, (1)

где 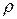- плотность жидкости, 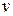- скорость истечения жидкости из отверстия, 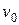- скорость опускания свободной поверхности жидкости в сосуде, 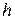- ее высота, отсчитываемая от уровня отверстия. Согласно теореме о неразрывности струи 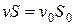. Отсюда и из уравнения Бернулли следует:

.

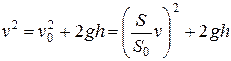Считая S << 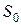, получаем, что скорость вытекания жидкости из отверстия равна

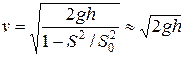. (2)

Это известная формула Торричелли.

Скорость опускания свободной поверхности жидкости в сосуде определяется выражением:

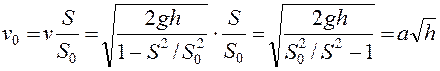, (3)

где коэффициент

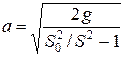. (4)

Так как скорость 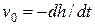, то получаем дифференциальное уравнение:

.

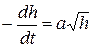Проинтегрируем его:

,

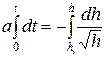где 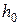- высота свободной поверхности жидкости в начальный момент времени 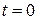. Имеем: 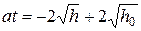. Отсюда следует, что высота свободной поверхности жидкости уменьшается, оставаясь пропорциональной квадрату времени:

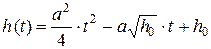. (5)

При выводе этих формул мы не учитывали вязкость жидкости.