Нечеткие отношения

Пусть P - четкое декартово произведение n множеств E₁, E₂,..., E_n. Нечеткое подмножество четкого множества называется n-арным нечетким отношением R _n на P:

R_n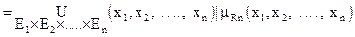

где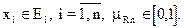

Величина m_Rn есть мера того, что совокупность (x₁, x₂,...,x_n) принадлежит отношению R _n. Знак U в данном случае обозначает объединение соответствующих одноточечных множеств (x₁, x₂,..., x_n).

На практике чаще других используется бинарное нечеткое отношениеR ₂, заданное на двух множествах, например, X и Y:

R ₂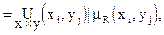

где m_R: X ´ Y ® [x,1].

Бинарное отношение может рассматриваться в качестве двухместного предиката.

Примеры нечетких отношений: "расстояние в пространстве значительно больше 1м" - тернарное отношение на множестве точек трехмерного пространства; "X - дальний родственник Y" - бинарное отношение на множестве людей.

Нечеткие бинарные отношения удобно задавать в виде матрицы. Например, R ₂ - нечеткое отношение "X значительно больше Y", заданное на множествах E_x = (4,8,10) и E_y= (2,3,4) может быть задано следующим образом:

2 3 4

R _{2 =}

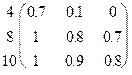
Содержательно это означает, например, следующее: со степенью уверенности лишь 0.7 можно утверждать, что 4 значительно больше 2; но 8 значительно больше 3 со степенью уверенности 0.8.

Нечеткому бинарному отношению можно поставить в соответствие нечеткий граф. Нечетким графом G на множествах E₁ и E₂ называется такое нечеткое подмножество, что

"(x_i,y_j) Î E₁ ´ E₂: m _G (x_i,y_j) Î M

где M - множество принадлежностей элементов множества E₁ ´ E₂.

Наглядным изображением нечеткого графа могут служить различные размытые изображения. Над нечеткими отношениями можно определить те же операции, что и над четкими отношениями [90].