Операции над нечеткими множествами

1. Дополнение. Пусть нечеткие множества A и B имеют единое базовое множество E. Нечеткое множество B является дополнением нечеткого множества A, (записывается B = ù A), если

"x Î E: m _B (x) = 1 - m _A (x).

Например, если

A = {(x₁ú0.2), (x₂ú0.7), (x₃ú1), (x₄ú0.4), (x₅ú0)},

то

ùA = {(x₁ú0.8), (x₂ú0.3), (x₃ú0), (x₄ú0.6), (x₅ú1)}.

2. Объединение. Объединением двух нечетких множеств A и B, заданных на одном и том же базовом множестве E называется нечеткое множество C = A È B, содержащее и Aи B, причем функция принадлежности определяется по правилу

" х Î E: m _C (х) = max(m _A (х),m _B (х))

Пример 2. Пусть A = {(x₁ú0.4), (x₂ú0.7), (x₃ú0.9)} и B = {(x₁ú0.5), (x₂ú0.3), (x₃ú1)}.

Тогда C = A È B = {(x₁ú0.5), (x₂0.7), (x₃ú1)}.

3. Пересечение. Пересечением двух нечетких множеств A и B, заданных на одном и том же базовом множестве E называется нечеткое множество D = A Ç B, содержащие и A и B, причем функция принадлежности определяется по правилу

"x E: m _D (x) = min(m _A (x),m _B (x)).

Для нечетких множеств из примера 2 имеем

D = A Ç B = {(x₁ú0.4), (x₂ú0.3), (x₃ú0.9)}

Наглядное представление операций объединения и пересечения двух нечетких множеств заданных на непрерывном подмножестве дают схемы, родственные диаграммам Вьенна - Эйлера, которые представлены на рис. 3.10. Границы штрихованных областей изображают графики функций принадлежности соответствующих нечетких множеств.

	Рис. 3.10. Иллюстрация операций объединения и пересечения нечетких множеств.

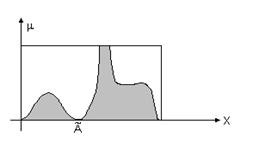
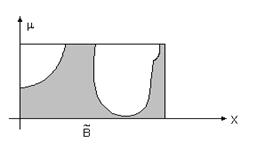
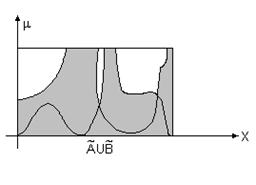
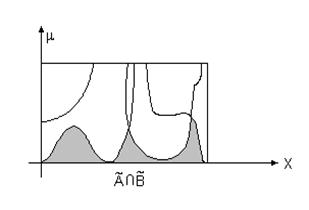
4. Произведение. Произведением двух нечетких множеств A ´ B, заданных на одном и том же базовом множестве E называется такое нечеткое множество

F = A ּ B, функция принадлежности которого определяется по правилу

"x Î E: m _F (x) = m _A (x)ּm _B (x)

Для нечетких множеств из примера 2 имеем

F = A ּ B = {(x₁ú0.2), (x₂ú0.21), (x₃ú0.90}

5. Сумма. Суммой двух нечетких множеств A и B, заданных на одном и том же базовом множестве E называется нечеткое множество H = A + B, содержащие множества A и B, причем функция принадлежности определяется по правилу

" х Î E: m _H (х) = m _A (х) + m _B (х) - m _A (х)ּm _B (х)

Для нечетких множеств из примера 2 имеем

H = A + B = {(x₁ú0.7), (x₂ú0.79), (x₃ú1)}.

Замечание. Операции умножения и суммирования нечетких множеств употребляются значительно реже, чем операции пересечения и объединения, поскольку для них не выполняются некоторые свойства, в том числе и такое, как дистрибутивность.

6. Разность. Разностью двух множеств A и B, заданном на одном и том же базовом множестве E, называется нечеткое множество G = A - B = A Ç ù B, причем функция принадлежности определяется по правилу

" х Î E: m _G (х) = min(m _A (х), 1 - m _B (х))

Для нечетких множеств из примера 2 имеем

G = A - B = {(x₁ú0.47), (x₂ú0.7), (x₃ú0.1)}.

7. Возведение в степень. Пусть задано нечеткое множество A, заданное на базовом множестве E. Возведением в неотрицательную степень "a" нечеткого множества A называется нечеткое множество K = A ^a, функция принадлежности которого m _K (х) определяется по правилу

m _K (х) = (m _A (х))^a

Возведение нечеткого множества в квадрат называется операцией концентрирования

A ² º CON(A).

Извлечение корня квадратного из нечеткого множества, рассматриваемого как возведение в степень 0.5, называется операцией растяжения

A ^0.5 = DIL(A).

Так, например, если

A = {(x₁ú0.4), (x₂ú0.7), (x₃ú0.9)},

то

CON(A) = {(x₁ú0.16, (x₂ú0.49), (x₃ú0.81)},

DIL(A) = {(x₁ú0.63), (x₂ú0.84), (x₃ú0.95)}.

Нечетким евклидовым расстоянием между двумя нечеткими множествами A и B называется величина

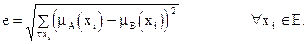
Ближайшим к данному нечеткому множеству A называется четкое множество A, расположенное на наименьшем евклидовом расстоянии от A. Это множество определяется функцией принадлежности, формируемой по правилу

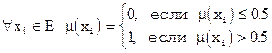
Пример 3. Пусть заданы два множества:

A = {(x₁ú0), (x₂ú0.1), (x₃ú0.3), (x₄ú0.7), (x₅ú0.8), (x₆ú0.9), (x₇ú1)}

и

B = {(x₁ú0), (x₂ú0), (x₃ú0), (x₄ú0.6), (x₅ú0.8), (x₆ú1), (x₇ú1)}.

Тогда e(AB)= 0.346, а ближайшее к нечеткому множеству A является четкое множество A = {(x₁ú0), (x₂ú0), (x₃ú0), (x₄ú1), (x₅ú1), (x₆ú1), (x₇ú1)}.

В теории нечетких множеств имеет место принцип обобщения, который можно записать следующим образом:

f({xúm _A (x)}) = {f(x)úm _A (x)}

где A - нечеткое множество; f - некоторое отображение X ® Y.

Например, если y = x² + 3 и A = {(1ú0.4), (2ú0.6), 3ú0.9}, то f(A) = {(4ú0.4), (7ú.0.6), (12ú0.9)}.

Этот принцип открывает возможности вводить функциональные описания на нечетких множествах, что имеет важное значение в приложениях теории нечетких множеств.