Следствие 1. Силу, приложенную к абсолютно твердому телу, можно переносить в любую точку ее линии действия. При этом действие силы на тело не изменится.
Доказательство:
Пусть на твердое тело действует сила 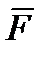 , приложенная к точке А (рис. 1.4). Приложим в некоторой точке В линии действия силы F систему сил {
, приложенная к точке А (рис. 1.4). Приложим в некоторой точке В линии действия силы F систему сил { 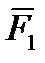 ,
,  } <=> 0, что допускается на основании Аксиомы 2. Примем
} <=> 0, что допускается на основании Аксиомы 2. Примем 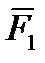 =
= 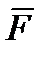 =
=  . В результате получим систему сил {
. В результате получим систему сил { 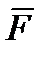 ,
, 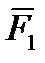 ,
,  } <=>
} <=> 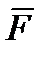 .
.
Заметим, что { 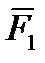 ,
,  } <=> 0, на основании аксиомы 2 эту систему сил можно отбросить. Получаем
} <=> 0, на основании аксиомы 2 эту систему сил можно отбросить. Получаем 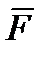 <=>{
<=>{ 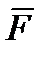 ,
, 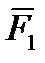 ,
,  } <=>
} <=> 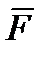 .
.
Вывод: Сила является скользящим вектором.
Следствие 2. Теорема о необходимом условии равновесия тела, находящимся под действием трех непараллельных сил, лежащих в одной плоскости.
Если свободное тело находится в состоянии равновесия под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
Доказательство:
Пусть к телу приложены три силы 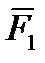 ,
,  ,
, 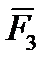 . {
. { 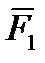 ,
,  ,
, 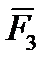 } <=> 0. Поскольку линии действия сил непараллельны, то любые две из них (пусть
} <=> 0. Поскольку линии действия сил непараллельны, то любые две из них (пусть 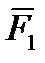 и
и  ) пересекутся в некоторой точке О. Перенесем F1 и F2 в точку О и заменим эти силы равнодействующей
) пересекутся в некоторой точке О. Перенесем F1 и F2 в точку О и заменим эти силы равнодействующей 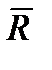 . Получим {
. Получим { 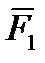 ,
,  ,
, 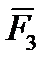 } <=> {
} <=> { 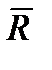 ,
, 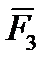 }, а для того чтобы тело находилось в равновесии необходимо выполнение условия:
}, а для того чтобы тело находилось в равновесии необходимо выполнение условия: 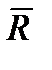 =
= 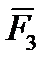 , и они должны быть направлены по одной прямой в противоположные стороны. То есть линия действия силы
, и они должны быть направлены по одной прямой в противоположные стороны. То есть линия действия силы 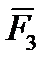 должна проходить через точку пересечения линий действия сил
должна проходить через точку пересечения линий действия сил 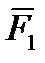 и
и  .
.
|
|

|
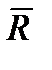
|
| О |
Рис. 1.4
 2015-04-20
2015-04-20 385
385








