2015-04-20
531
Теорема. Система сходящихся сил на плоскости эквивалентна равнодействующей, приложенной в точке схода и равной геометрической сумме сил.
Доказательство:
Пусть {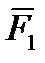 
, 
, 
, … 
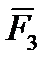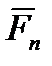} система сходящихся сил, а точка О – точка схода (рис. 2.10). Пользуясь аксиомами статики, приведем систему сил к точке схода, и заменим систему сил { , } <=> 
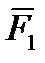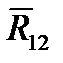, то есть получим { 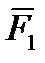, , , 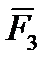… 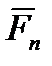} эквивалентную { 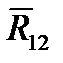, , , 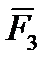… 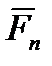}. Затем заменим { , } <=> 
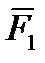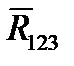и т. д., в итоге получим одну силу приложенную в точке О, то есть { , , , … } <=> 
.
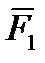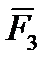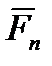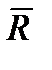| F1 |
| F2 |
| F3 |
| Fn |
| O |
| R12 |
| R123 |
| R |
Рис. 2.10
Аналитический способ нахождения равнодействующей
Геометрический способ нахождения равнодействующей системы сил сопряжен с определенными трудностями, особенно в случае большого числа сил. Поэтому предпочтительнее аналитический метод нахождения равнодействующей.
Пусть { 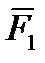, , , 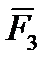… 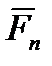} система сходящихся сил на плоскости имеет равнодействующую 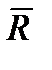. Обозначим через 
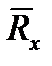и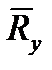 
проекции этой равнодействующей на оси системы координат XOY, а через 
, 
; 
, 
;... 
, 
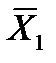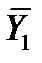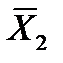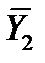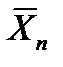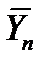;проекции сил 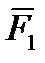, , , 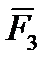… 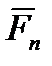на те же оси. Из математики известно, что проекция суммы векторов на какую – либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Тогда
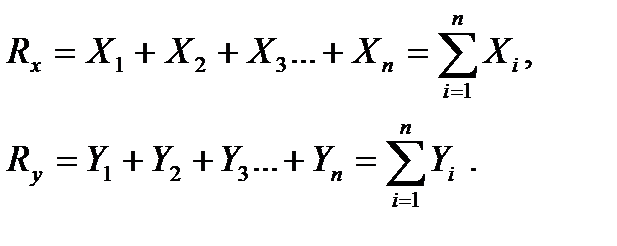(2.2)
Модуль равнодействующей равен:
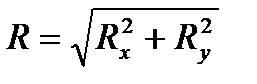. (2.3)
Направляющие косинусы вектора R можно найти по формулам
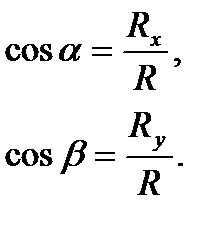(2.4)
Условие равновесия системы сходящихся сил в геометрической и аналитической форме.
В геометрической форме: Для равновесия свободного твердого тела, находящегося под действием плоской сходящейся системы сил необходимо и достаточно, чтобы силовой многоугольник был замкнут (рассмотрим на примере плоской сходящейся системы сил { , , ,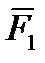 
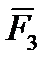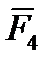} (рис. 2.11).
| F1 |
| F2 |
| F3 |
| F4 |
| F1 |
| F2 |
| F3 |
| F4 |
| О |
Рис. 2.11
В аналитической форме: Для равновесия свободного твердого тела, находящегося под действием плоской сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из осей равнялась нулю:
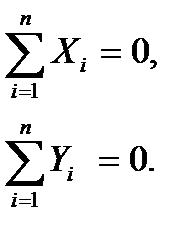(2.5)
