Работа сил электрического поля. Потенциал

Работа перемещения заряда. На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила
F = q E. При перемещении заряда на отрезке d l силами поля совершается работа

d A = F d l =q E d l cos (E, d l ).

При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна

.

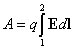Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого

.

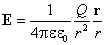Проекция отрезка d l на направление вектора E (рис. 1.5) есть d r = d l cos (E, d l).

Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом:

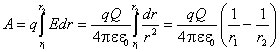
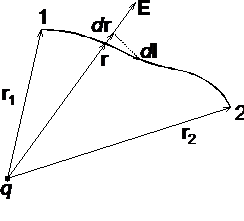Отсюда следует, что работа сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q. Если оба заряда, q и Q, положительны, то работа сил поля положительна при удалении зарядов и отрицательна при их взаимном сближении.

Для электрического поля, созданного системой зарядов Q ₁, Q ₂,¼, Q_n, работа перемещения заряда q равна алгебраической сумме работ составляющих сил:

.

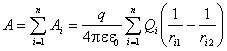Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q, находящегося в электрическом поле, созданном другим точечным зарядом Q, получим

,

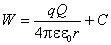где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥), тогда постоянная C = 0 и предыдущее выражение принимает вид

.

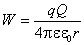При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную. В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q:

.

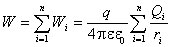Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристикаэлектростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда (для любой системы единиц; подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

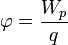
Напряжённость электростатического поля 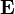и потенциал 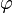связаны соотношением^[1]

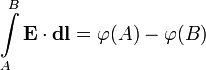
или обратно^[2]:

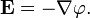
Здесь — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля 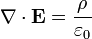, легко увидеть, что электростатический потенциал удовлетворяетуравнению Пуассона. В единицах системы СИ:

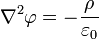
где 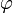— электростатический потенциал (в вольтах), 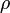— объёмная плотность заряда (в кулонах на кубический метр), а 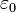— диэлектрическая проницаемость вакуума (вфарадах на метр).