Потенциал электростатического поля, разность потенциалов. Потенциал точечного заряда

Рассмотрим поле, создаваемое неподвижным зарядом q. В любой точке этого поля на точечный заря действует сила Кулона 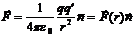. Так как сила является центральной, поле этой силы консервативно. Следовательно работа, которую совершается силами поля над зарядом при перемещении из одной точки в другую не зависит от пути.

Работа равна , dl – элементарное перемещение. . - потенциальная энергия. Работа консервативного поля может быть представлена как убыль потенциальной энергии. .

Будем вносить в поле разные пробные заряды. Разные пробные заряды будут обладать в одной и той же точке разными потенциальными энергиями. Однако отношение потенциальной энергии к пробному заряду остается одинаковой для всех зарядов. Величина называется потенциалом поля в данной точке и является еще одной характеристикой поля наряду с напряженностью E. Из формулы следует, что потенциал численно равен . – потенциал поля точечного заряда. Потенциал системы n зарядов равен 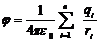: равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности. Заряд находящийся в точке поле с потенциалом φ обладает потенциальной энергией 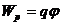. Следовательно работа поля над зарядом q может быть выражена формулой . Таким образом, работа, совершаемая над зарядом полем равна произведению заряда на разность потенциалов в начальной и конечной точках. Если заряд q из точки с потенциалом φ удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна нулю .

Следовательно, потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность. Единицы потенциала 1В = 1Дж/1Кл.

Связь между напряженностью поля и его потенциалом

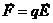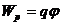, , , следовательно и .

Напряженность поля точечного заряда , а потенциал поля точечного заряда .