Потенциальное векторное поле

Определение. Векторное поле называется потенциальным в области G, если существует такая скалярная функция , что её градиент равен вектору , т.е. .

Функция называется скалярным потенциалом векторного поля . Если , то из определения следует, что

Пусть функции имеют непрерывные частные производные в односвязной области G. Тогда для потенциального поля можно доказать эквивалентность следующих утверждений.

1) Поле является потенциальным тогда и только тогда, когда (15.6)

Для плоского поля: . Это необходимые и достаточные условия потенциальности поля.

2) Циркуляция потенциального векторного поля по любому замкнутому контуру равна нулю.

3) В области существует скалярная функция , полный дифференциал которой совпадает с подынтегральным выражением криволинейного интеграла, т. е. В этом случае функция определяется не однозначно, а с точностью до постоянного слагаемого, т.к.

4) Криволинейный интеграл потенциального векторного поля не зависит от пути, соединяющего две произвольные точки и , а зависит только от положения этих точек. Имеет место формула Ньютона-Лейбница.

, (15.7)

т.е. работа в потенциальном поле не зависит от выбора пути между точками А и В, и равна разности потенциалов в этих точках.

Пример 15.2. Убедимся в том, что поле

Рисунок 12

является потенциальным, найдём потенциал поля U и вычислим работу, совершаемую этим полем при перемещении материальной точки из в .

Решение. Поле определено в каждой точка пространства . Проверим потенциальность поля (см. (15.6)):

условия выполнены, поле потенциально.

 

Рисунок 15.3

 

Для вычисления потенциала воспользуемся тем, что линейный интеграл в таком поле не зависит от пути интегрирования и может быть вычислен по формуле Ньютона-Лейбница. Пусть точка - начало пути, а некоторая точка - конец пути. Вычислим интеграл по контуру, состоящему из отрезков прямых, параллельных координатным осям (см.Рисунок 15.3). .

Уравнения частей контура: , , .

Тогда , .

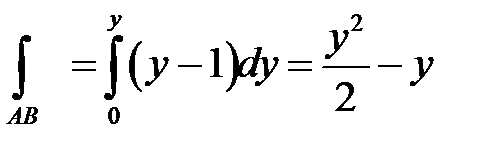В итоге получаем: .

Теперь тот же интеграл вычислим по формуле Ньютона-Лейбница: .

Сравним результаты:

Из полученного равенства следует, что , а . Потенциал данного поля найден.

Найдём работу, совершаемую векторным полем при перемещении точки из в 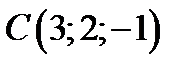. В потенциальном поле работа равна разности потенциалов в конечной и начальной точках пути (см .(15.7)), т. е. Вычислив значения потенциала в точках, получаем ответ: работа .