Метод Алмона

Рассмотрим общую модель с распределенным лагом, имеющую конечную максимальную величину лага 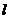, которая описывается соотношением: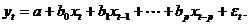

В методе Алмона предполагается, что в исследуемой модели имеет место полиномиальная структура лага, т.к. зависимость коэффициентов регрессии 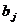от величины лага описывается полиномом k-й степени. Таким образом, лаги Алмон – лаги, структуру которых можно описать с помощью полиномов.

Формально модель зависимости коэффициентов 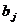от величины лага j в форме полинома можно записать в следующем виде: 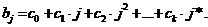Тогда каждый из коэф-ов 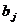модели можно выразить след. обр.:

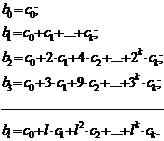
Тогда модель с распределенным лагом примет вид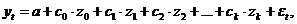

где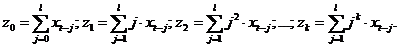

Процедура применения метода Алмон для расчета параметров модели с распределенным лагом проводится по следующей схеме:

1.Устанавливается макс. величина лага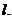

2.Определяется степень полинома k, описывающего структуру лага.

3. Рассчитывается значение переменных с z0 до zk.

4. Определяются параметры уравнения линейной регрессии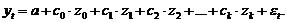

5.Рассчитываются параметры b исходной модели с распределенным лагом с помощью ранее найденных соотношений.

Проблемы применения метода Алмон:

- величина лага 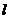должна быть известна заранее; при определении лучше исходить из максимально возможного лага;

- необходимо установить степень полинома (должна быть на 1 больше числа экстремумов в структуре лага);

- переменные z, определяемые как линейные комбинации исходных переменных х, коллелируют между собой, если существует высокая связь между исходными переменными х.

Преимущества метода Алмон:

- он достаточно универсален и может быть применен для моделирования процессов, которые характеризуются разнообразными структурами лагов;

- при относительно небольшом количестве переменных можно построить модели со степенью полинома 2 или 3, которые не приводят к потере значительного числа степеней свободы.

- можно построить модели с распределенным лагом любой длины.