Доказательство теоремы

1 2 3 4 5 6 7

Теорема.

Если 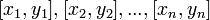- последовательность стягивающихся отрезков, то 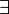! точка, принадлежащая всем этим отрезкам.

Доказательство теоремы.

, .

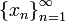Множество 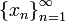ограничено сверху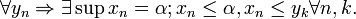

Множество ограничено снизу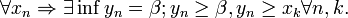

, ; ; .

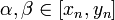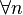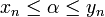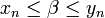Покажем, что .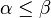

Предположим, что 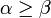. Тогда 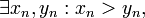чего быть не может.

Предположим, что 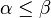. Тогда 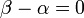. Положим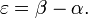

: . (*)

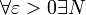
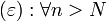
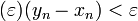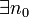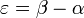
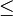
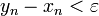Значит,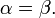

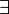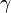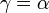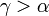Предположим, что другая точка , общая для всех отрезков: 1) ;2) ;3) 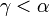. Но пункты 2), 3) невозможны, т.к. (*).

лемма о конечности покрытыми отрезками интервалами.

Чтобы сформулировать лемму Гейне — Бореля в общем случае, введем понятие покрытия ^[3]. Система множеств

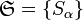
где индекс 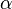пробегает некоторое множество 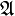, называется покрытием множества 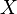, если

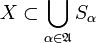
Если некоторая часть покрытия 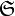, скажем 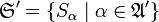, где 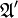— подмножество 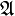, сама образует покрытие множества 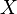, то 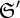называется подпокрытием покрытия 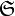множества .

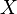Теперь сформулируем лемму Гейне — Бореля в общем виде.

Пусть 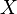— замкнутое ограниченное множество в пространстве 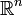. Тогда из всякой системы открытых множеств, покрывающих множество 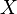, можно выделить конечную подсистему, также покрывающую множество .

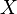Кратко говорят так: всякое открытое покрытие замкнутого ограниченного множества в пространстве 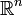содержит конечное подпокрытие. При этом покрытие называется открытым, если оно состоит из открытых множеств.

Имеет место и обратное предложение: для того чтобы всякое открытое покрытие множества 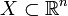содержало конечное подпокрытие необходимо, чтобы множество 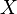было замкнутым и ограниченным. Однако леммой Гейне — Бореля называют лишь прямое утверждение, то есть достаточные условия существования конечного подпокрытия.

Окрестность точки:

Пусть x0 – любое действительное число (точка на числовой прямой). Окрестностью точки x0 называеться любой интервал (а;b), содержащий точку x0. В частности, интервал (x0-ἐ,x0+ἐ), где ἐ>0 называеться, называеться ἐ- окрестностью точки x0.

Лемма о предельной точке бесконечного ограничения множества в R:

Пусть А вложена в R – ограниченное бесконечн мно-во,

Пусть А волеженно [a,b]=> любое с принадлежащее А предельная точка мн-ва.

6 Равномощные множества

A,B-произвольные мн-ва А ранвомошно B если B:ó существ отображение А к B – взаимноподзначные отображение.

Счётное множество

А- счётное:óA равномощно множеству натуральных чисел.

Теорема Кантора:

Любое множество менее мощно, чем множество всех его подмножеств.

]Доказательство

Предположим, что существует множество 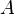, равномощное множеству всех своих подмножеств 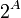, то есть, что существует такая биекция 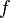, ставящая в соответствие каждому элементу множества 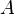некоторое подмножество множества .

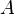Рассмотрим множество 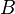, состоящее из всех элементов 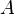, не принадлежащих своим образам при отображении 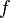(оно существует по аксиоме выделения): .

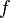биективно, а 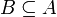, поэтому существует 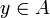такой, что .

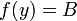Теперь посмотрим, может ли 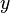принадлежать .

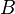Если 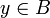, то 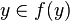, а тогда, по определению , .

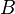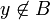И наоборот, если 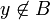, то 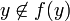, а следовательно, 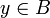. В любом случае, получаем противоречие.

Следовательно, исходное предположение ложно и 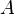не равномощно .

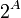Заметим, что 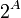содержит подмножество, равномощное 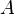(например, множество всех одноэлементных подмножеств 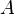), а тогда из только что доказанного следует .

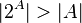Под числовой последовательностью x1,x2,x3,..xn,… понимается функция

xn=f(n)

заданная на множестве N натуральных чисел. Кратко последовательность обозначаеться в виде {xn} или xn,n принадлежит N Число х1 называеется первым членом элементом последовательности хn общим или n-м членом последовательности.

Предел числовой последовательнсоти.

Число а называют пределом последовательности {xn}, если для лобого положительного числа ἐ найдёться такое натуральное число N, что при всех n>N выполняеться неравенство

│xn-a│<ἐ

Единственность предела. Если предел последовательсности существует, то он единственен.

Число 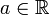называется пределом числовой последовательности 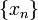, если последовательность 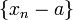является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

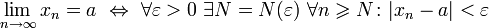
В случае, если у числовой последовательности существует предел в виде вещественного числа 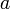, её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

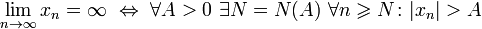
Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

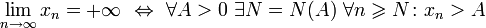
Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.