Пусть даны функции 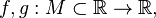 и
и 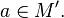 .
.
· Одна и та же функция в одной и той же точке может иметь только один предел.
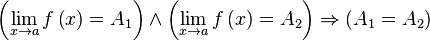
Доказательство [показать]
· Сходящаяся функция локально сохраняет знак. Более обще,
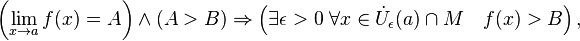
где 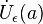 — проколотая окрестность точки
— проколотая окрестность точки 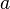 .
.
· В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
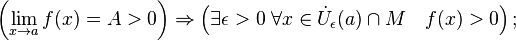
· Сходящаяся функция локально ограничена в окрестности предельной точки:
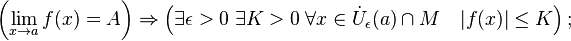
· Отделимость от нуля функций, имеющих предел, отличный от нуля.
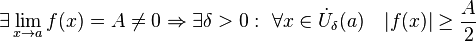
· Операция взятия предела сохраняет нестрогие неравенства.
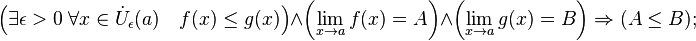
· Правило двух милиционеров
· Предел суммы равен сумме пределов:
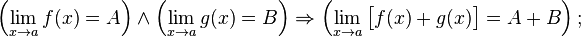
· Предел разности равен разности пределов:
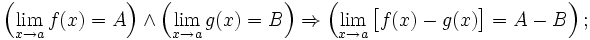
· Предел произведения равен произведению пределов:
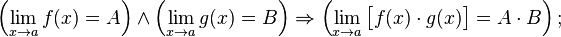
· Предел частного равен частному пределов.
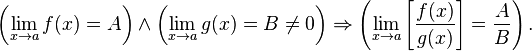
Бесконечные пределы в конечной точке
Кроме конечных пределов существуют и бесконечные.
Функция f (x), определенная в некоторой окрестности точки а из множества действительных чисел, кроме, быть может, самой точки а, имеет в этой точке бесконечный предел, если для каждого ε > 0 найдется такая δ - окрестность точки а, что всех х, удовлетворяющих условию 0 < | x - a | < δ, х ≠ а выполняется неравенство | f (x) | > ε.
В этом случае записывают:
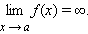
Функцию f(x) принято называть бесконечно большой при х → а, а прямую х = а - вертикальной асимптотой.
Пример. Рассмотрим функцию
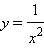
Эта функция определена при х ≠ 0. Если х → 0, то | f(x) | неограниченно возрастает, т.е.
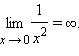
Предел в бесконечности
Число А называется пределом функции f(x) при x → + ∞, если для каждого ε > 0 существует такое δ > 0, что всех x > δвыполняется неравенство | f (x) – A | < ε. И это записывается как
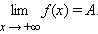
Аналогично формулируется определение предела при x, стремящемся к минус бесконечности: число А называется пределом функции f(x) при x → - ∞, если для каждого ε > 0 существует такое δ > 0, что всех x < - δ выполняется неравенство | f (x) – A | < ε.
Число А называется пределом функции f(x) при x → ∞, если для каждого ε > 0 существует такое δ > 0, что всех | x | > δ выполняется неравенство | f (x) – A | < ε.
При решение некоторых пределов полезно обращаться к так называемым замечательным пределам:
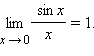
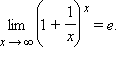
Из замечательных пределов и свойств обратной функции вытекают следующие важные пределы (при a > 0, a ≠ 1):
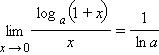
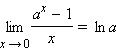

Односторонние пределы
Пусть задано а - действительное число.
Число А1 является пределом слева функции f (x) в точке а, для любого ε > 0 существует δ > 0 такое, что для любого x из интервала (а - δ; а) выполняется неравенство | f(x) - A1 | < ε. В этом случае пишут lim f(x) = A1 при x → a - 0.
Число А2 называется пределом справа функции f (x) в точке а, если для любого ε > 0 существует δ > 0 такое, что для любого x из интервала (а; а + δ) выполняется неравенство | f(x) - A2 | < ε. В этом случае пишут
lim f(x) = A2 при x → a + 0. При а = 0 принята краткая запись х → +0 (х → -0) вместо х → 0 + 0 (х → 0 - 0).
Числа А1 и А2 принято называть о дносторонними пределами.Эти пределы характерезуют поведение функции справа и слева от точки А.
Из всего сказанного выше получается,что функция f (x) имеет предел в точке а из множества действительных чисел тогда и только тогда, когда в этой точке она имеет односторонние пределы и эти пределы совпадают.

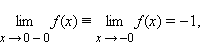
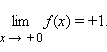
Приведем пример, когда односторонние пределы не совпадают. Тогда говорят, что предела в рассматриваемой точке нет.
Пусть 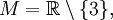 и задана функция
и задана функция
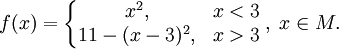
Рассмотрим график заданной функции
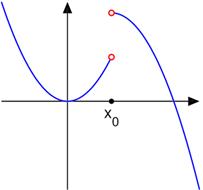
Где х0 = 3. Ясно,что
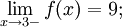
Установили, что в точке х0 = 3 односторонние пределы не совпадают. Следовательно, предела рассматриваемой функции в точке х0 = 3 не существует.
. Критерий существования двустороннего предела:
Двухсторонний предел существует если существуют и равны между собой односторонние пределы.
 2015-04-20
2015-04-20 1330
1330
