Теорема 13. Если монотонная последовательность 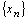 ограничена, то она сходится.
ограничена, то она сходится.
Доказательство. Так как последовательность 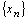 ограничена, то множество ее элементов имеет точные верхнюю
ограничена, то множество ее элементов имеет точные верхнюю 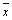 и нижнюю
и нижнюю 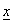 грани. Пусть
грани. Пусть 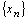 – неубывающая последовательность и
– неубывающая последовательность и 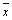 – точная верхняя грань множества ее элементов. Это означает, что для любого числа
– точная верхняя грань множества ее элементов. Это означает, что для любого числа 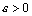 можно указать такой элемент
можно указать такой элемент 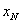 , что
, что 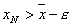 и
и 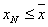 . Эти два неравенства равносильны неравенству
. Эти два неравенства равносильны неравенству 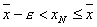 или
или 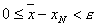 . Так как
. Так как 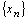 – неубывающая последовательность, то при
– неубывающая последовательность, то при 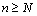 выполняется
выполняется 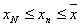 или
или 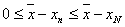 . Это означает, что при
. Это означает, что при 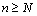 выполняется
выполняется 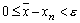 или
или 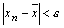 . Таким образом,
. Таким образом, 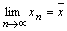 . Аналогично доказывается случай, когда
. Аналогично доказывается случай, когда 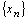 – невозрастающая последовательность.
– невозрастающая последовательность.
Замечание 1. Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие ее сходимости. Действительно, по теореме 8 сходящаяся монотонная последовательность ограничена.
Замечание 2. Сходящаяся последовательность может и не быть монотонной. Например, последовательность 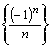 сходится к числу ноль, но не является монотонной.
сходится к числу ноль, но не является монотонной.
Замечание 3. Если последовательность 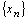 неубывающая сходящаяся и
неубывающая сходящаяся и 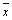 - ее предел, то для всех номеров n выполняется неравенство
- ее предел, то для всех номеров n выполняется неравенство 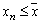 . Аналогично, если
. Аналогично, если 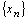 невозрастающая сходящаяся последовательность и
невозрастающая сходящаяся последовательность и 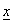 – ее предел, то для всех номеров n справедливо
– ее предел, то для всех номеров n справедливо 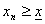 .
.
 2015-04-20
2015-04-20 5990
5990
