Определения. Допустим, у нас есть бесконечно малые при одном и том же 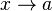величины 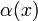и (либо, что не важно для определения

Допустим, у нас есть бесконечно малые при одном и том же величины и 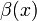(либо, что не важно для определения, бесконечно малые последовательности).

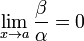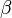· Если , то — бесконечно малая высшего порядка малости, чем 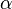. Обозначают .

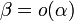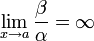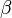· Если , то — бесконечно малая низшего порядка малости, чем 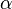. Соответственно .

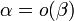· Если 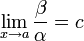(предел конечен и не равен 0), то 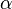и 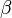являются бесконечно малыми величинами одного порядка малости.

Это обозначается как 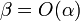или 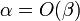(в силу симметричности данного отношения).

· Если 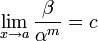(предел конечен и не равен 0), то бесконечно малая величина 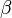имеет 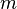-й порядок малости относительно бесконечно малой .

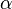Для вычисления подобных пределов удобно использовать правило Лопиталя.