2015-04-20
267
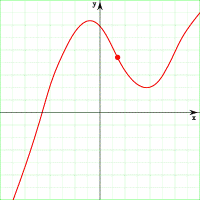
ε-δ определение
Пусть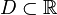 
и 
.
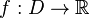Функция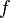 
непрерывна в точке 
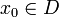, если для любого 
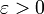существует 
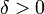такое, что для любого
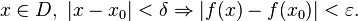
Функция 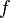непрерывна на множестве 
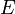, если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция 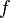класса 
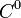и пишут: 
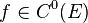или, подробнее, 
.
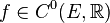Комментарии
· Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция 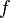непрерывна в точке 
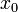, предельной для множества 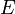, если 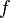имеет предел в точке 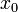, и этот предел совпадает со значением функции 
.
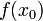· Функция непрерывна в точке, если её колебание в данной точке равно нулю.
