Устранимые точки разрыва

Если предел функции существует, но он не совпадает со значением функции в данной точке:

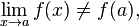
тогда точка 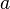называется точкой устранимого разрыва функции 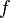(в комплексном анализе — устранимая особая точка).

Если «поправить» функцию 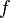в точке устранимого разрыва и положить 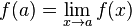, то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.