Очевидно, что справедлива следующая теорема

Теорема 1: Функция y=f(x) имеет производную в точке 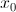тогда и только тогда, когда в этой точке существуют и равны между собой производные функции справа и слева. Причем

.

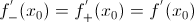Следующая теорема устанавливает связь между существованием производной функции в точке 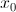и непрерывностью функции в этой точке.

ТЕОРЕМА (необходимое условие существования производной функции в точке). Если функция y = f(x) имеет производную в точке 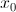, то функция f(x) в этой точке непрерывна.

ДОКАЗАТЕЛЬСТВО

Пусть существует 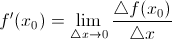. Тогда

,

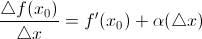где 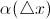– бесконечно малая при .

⇒ ;

⇒

.

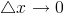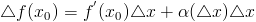Но это означает, что функция f(x) непрерывна в точке 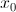(по геометрическому определению непрерывности). ∎