2015-04-20
468
Введем обозначение:
R (x)= f (x)- Pn (x)= f (x)–[ f (x 0)+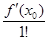 
(x – x 0)+ … + 
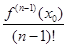(x – x 0) n -1+ 
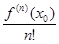(x – x 0) n ].
Надо доказать, что R (x) = o ((x – x 0) n). Мы докажем это с помощью правила Лопиталя.
Требуется доказать, что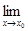 
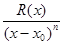= 0. (5)
Отметим прежде всего, что в силу условия теоремы сама функция f (x) и ее производные f ’(x), …, f ( n -1)(x) непрерывны в точке x 0. Поэтому, используя условие (1), получаем:
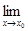R (x) = 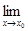[ f (x) - Pn (x)] = f (x 0) - Pn (x 0)] = 0. (6)
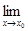R ’(x) = 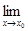[ f ’(x) – P ’ n (x)] = f ’(x 0) – P ’ n (x 0)] = 0. (6’)
и так далее…
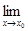R ( n -1)(x) = 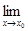[ f ( n -1)(x) – P ( n -1) n (x)] = f ( n -1)(x 0) – P ( n -1) n (x 0)] = 0. (6( n -1))
В силу (6) предел (5) является неопределенностью типа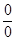 
. В силу (6’)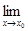 
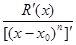также является неопределенностью типа 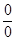. и так далее…
В силу (6( n -1))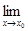 
= 
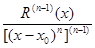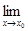
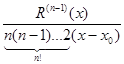снова является неопределенностью типа 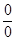. Для вычисления последнего предела рассмотрим выражение для R ( n -1)(x). R ( n -1)(x) = f ( n -1)(x) - f ( n -1)(x 0) - f ( n )(x 0)(x – x 0). Так как f ( n -1)(x) дифференцируема в точке x 0, то ее приращение в точке x 0 тожно представить в виде:
f (n -1)(x) - f (n -1)(x 0) =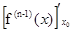 
×(x – x 0) + o (x – x 0) = f (n)(x 0)(x – x 0) + o (x – x 0).
Следовательно, R ( n -1)(x) = o (x – x 0), поэтому =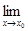 
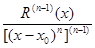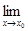
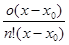= 0.
Таким образом, применяя к пределу (5) правило Лопиталя, получим:
|
|
|
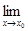
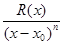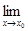
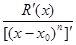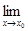
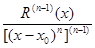= = … = = 0,
что и требовалось доказать.
